Inhaltsverzeichnis

1	Physikalische Grundlagen
	1.1	Die Kristallstruktur von GaAs
	1.2	Die elektronische Struktur von GaAs
	1.3	Eindimensionaler Transport

I	Herstellung der Proben

2	Vorstrukturierung der V-Gräben
	2.1	Ätzen der V-Gräben
		2.1.1	Experimentelle Durchführung
		2.1.2	Versuch mit einer -Maske

3	Wachstum der Quantendrähte
	3.1	Heterostrukturen
		3.1.1	Der Heteroübergang
		3.1.2	Modulationsdotierung
	3.2	Grundlagen der MOVPE
		3.2.1	Diffusionskontrolliertes Wachstum
		3.2.2	Diffusionsprozesse
	3.3	Wachsen von Quantendrähten in der MOVPE
		3.3.1	Wachsen auf V-Gräben
		3.3.2	Ausbilden des Quantendrahtes
	3.4	Konkrete Epitaxien
		3.4.1	Schichtfolge
		3.4.2	Umfang der gewachsenen Proben
	3.5	TEM-Aufnahmen

II	Optische Untersuchungen

4	Vorbemerkungen
	4.1	Photolumineszenz in Halbleitern
	4.2	Band-Band-Übergang
	4.3	Leistungsabhängigkeit
	4.4	Der eindimensionale Zustand

A	Danksagungen

Einleitung

Alle müssen mit dieser schwierigen Phase der Physik fertig werden.

– Steven Weinberg, Der Traum von der Einheit des Universums

Quantendrähte sind elektrische Leiter, deren Querschnitt so klein ist, daß die Teilchenwelle eines Elektrons in der Ebene des Querschnitts quantisiert wird. Während also die Dichte der Teilchen in Drahtrichtung nahezu konstant ist, bildet sie senkrecht dazu Bäuche und Knoten aus. Man spricht von einem eindimensionalen Zustand. Im Leiter hat man dann ein eindimensionales Elektronengas.

Zum einen sind die extrem kleinen Abmessungen interessant, zum anderen sagen einige theoretische Arbeiten eine besonders hohe Beweglichkeit der Ladungsträger in solchen Quantendrähten voraus. Beides macht sie attraktiv für eine noch kleinere Art von Chip-Strukturen, wo sie Signale mit weniger Platzverbrauch, weniger Wirkleistung und größerer Geschwindigkeit übermitteln könnten. Aber das ist alles ferne Zukunftsmusik.

[…]

Die Energie der Draht-Zustände ist – abgesehen von den beteiligten Materialien – zunächst einmal von den Ausmaßen des Quantendrahtes abhängig. Wird er dünner, werden die Energien größer, genau wie beim Teilchen im Potentialtopf. Gleichzeitig spielt auch die Konzentration von Ladungsträgern im Draht eine wichtige Rolle.

Ich habe in dieser Arbeit V-Graben Quantendrähte mittels der metall-organischen Gasphasen-Epitaxie (MOVPE) hergestellt. Der Draht besteht aus , das in ein Barrieren-Material aus $Al_{0,3}Ga_{0,7}As$ eingebettet ist. Ich habe dabei eine ganze Reihe nahezu identischer Proben produziert, bei denen lediglich die Drahtdicke und die Dotierung variiert wurden.

[…]

Kapitel 1: Physikalische Grundlagen

1.1 Die Kristallstruktur von GaAs

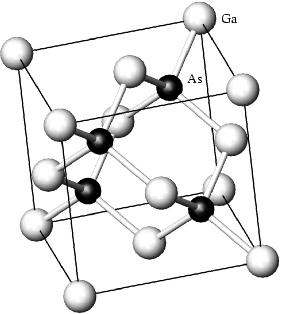
Die Elementarzelle von GaAs. (Die Kugel... (Für Original-Bitmap anklicken)

Abbildung 1.1: Die Elementarzelle von

. (Die Kugeln reräsentieren nicht die Atomradien; die geben lediglich die Lage der Schwerpunkte an.)

In Abbildung 1.1 sieht man die Elementarzelle von . Sie zeigt ein kubisch-flächenzentriertes (fcc‑)‚Gitter, Raumgruppe . Es gibt zwei Punktlagen: Das Gallium-Atom liegt auf , das Arsen-Atom auf . Sowohl das Gallium, als auch das Arsen bilden für sich ein kubisch flächenzentriertes Gitter, die beide gegeneinander um verschoben sind. (Siehe dazu auch Borchardt-Ott (1997).) Abbildung 1.1 zeigt die Elementarzelle, so wie sie in der Literatur meist dargestellt wird, aber man sollte beachten, daß man Ga und As gedanklich in der Struktur austauschen kann.

Bei allen Netzebenen und bei allen Raumrichtungen, die ich in dieser Arbeit angebe, verwende ich die Reihenfolge

bzw.

, wobei

in allen Abbildungen senkrecht nach oben weist und auch senkrecht zum Wafer steht. Die Waferoberfläche ist also eine

-Fläche. Alle Netzebenen der Form

liegen parallel zur

-Richtung,¹⁾ also derjenigen Richtung, in die die V-Gräben geätzt werden, und eine solche Netzebene schließt mit der Waferoberfläche einen Winkel ϑ ein mit

$ϑ_{(hhl)}=arctan\frac{h\sqrt{2}}{l}$

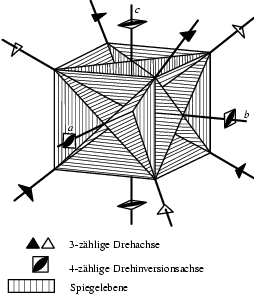
Symmetrie-Elemente der Punktgruppe ¯43m. Die
zwei verschie...

Abbildung 1.2: Symmetrie-Elemente der Punktgruppe

. Die zwei verschiedenen Symbole für die dreizähligen Achsen deuten an, daß diese Achsen zwei verschiedene Enden besitzen, also polar sind; das gilt ebenso für die

, obwohl nur ein Symbol. Aus Borchardt-Ott (1997, Kap. 7.1)

Die für Arbeiten mit Wafern wichtigsten Symmetrie-Elemente sind diejenigen, die senkrecht zur -Fläche liegen. Wie Abbildung 1.2 zeigt, gibt es drei dieser Art: Zwei Spiegelebenen, die auf dem Wafer in - und -Richtung verlaufen, sowie eine vierzählige Drehinversions-Achse in -Richtung. Eine enthält keine vierzählige, nur eine zweizählige Drehachse. Das ist der Grund, warum V-Gräben nur in -Richtung, nicht aber senkrecht dazu, geätzt werden können. Es gibt ausschließlich polare Drehachsen²⁾ und damit keine Inversionssymmetrie.

Doch nach welchem Mechanismus werden überhaupt die V-Gräben ausgebildet? Ohne die Beschreibung des Ätzens in Abschnitt 2.1 vorwegzunehmen, möchte ich hier auf die kristallographischen Aspekte eingehen.

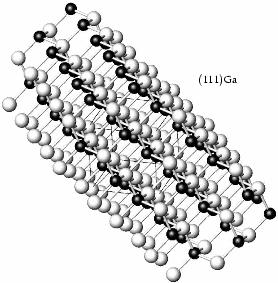
Blick in die Schichtstruktur von GaAs. ... (Für Original-Bitmap anklicken)

Abbildung 1.3: Blick in die Schichtstruktur von

. Am Ga erkennt man die typische Schichtfolge A–B–C–A. Oben rechts ist eine

Ga-Netzebene.

Abbildung 1.3 zeigt einen -Kristall fast senkrecht zur -Ebene. Damit ist diese Ansicht nicht ganz, aber fast in Richtung der V-Gräben. Man erkennt eine Schichtstruktur aus abwechselnd Gallium- und Arsen-Schichten. Oben rechts ist eine Ga-Netzebene, was bedeutet, daß es eine -Ebene ist, die mit Gallium-Atomen abschließt. Von dort wirkt auch die Ätze. Sie stoppt auf einer solchen Ga-Ebene, weil offensichtlich die Ga-Atome stärker als die As-Atome gebunden sind, was aus der Abbildung auch unmittelbar einsichtig wird: Jedes Ga-Atom wird von drei As-Atomen gehalten, wenn wir uns aber die oberste Ga-Schicht wegdenken, hätte jedes As-Atom nur ein Ga als nächsten Nachbarn. (Senkrecht zur -Ebene steht übrigens eine dreizählige Drehachse, die dadurch, daß sie polar ist, diese Asymmetrie überhaupt erst möglich macht.)

Es gibt allerdings auch rein chemische Gründe für dieses Verhalten, d. h. Gallium wird grundsätzlich wesentlich weniger stark von der Ätze gelöst als Arsen. Ätzt man V-Gräben in -Richtung, so stoppt der Vorgang nicht auf einer As-Ebene, obwohl dort die Bindungsverhältnisse äquivalent zu einer Ga-Ebene sind. Statt dessen wird extrem unterätzt bis zur nächsten Ga, die wegen der identisch zu einer Ga ist. (Kaluza 2000, Kap. 7.1)

Für das Ätzen von V-Gräben ist offensichtlich ebenfalls essentiell, daß eine -Ebene viel schneller als eine Ga-Ebene geätzt wird.³⁾ Anderenfalls müßte man extrem lange ätzen (und zahlreiche Defekte in Kauf nehmen), oder man würde sogar überhaupt keine V-Gräben erhalten.

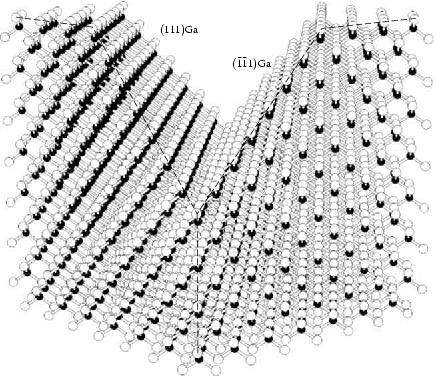
Eine in eine GaAs-Struktur geätzte Kerb... (Für Original-Bitmap anklicken)

Abbildung 1.4: Eine in eine

-Struktur geätzte Kerbe, abgeschlossen von zwei

-Netzebenen. Ich habe zur besseren Übersicht die vorderen Kanten hervorgehoben.

Die Abbildung 1.4 schließlich illustriert das Ergebnis eines typischen Ätzschrittes. Man sieht einen Würfel bestehend aus Elementarzellen, und wir schauen ungefähr in -Richtung, also über die Flächendiagonale des Würfels. Genau dort hat die Ätze gewirkt und einen V-Graben entstehen lassen, der von zwei äquivalenten Ga-Ebenen begrenzt ist (im Graben steht eine Spiegelebene!).

Im ist natürlich nur Gallium durch Aluminium zu ersetzen. Die Gitterkonstante von ist bei Zimmertemperatur um lediglich größer als die von . Ich benutze allerdings kein , sondern $Al_{0,3}Ga_{0,7}As$ . Nimmt man das Vegardsche Gesetz an,⁴⁾ wird der Unterschied noch kleiner.

1.2 Die elektronische Struktur von GaAs

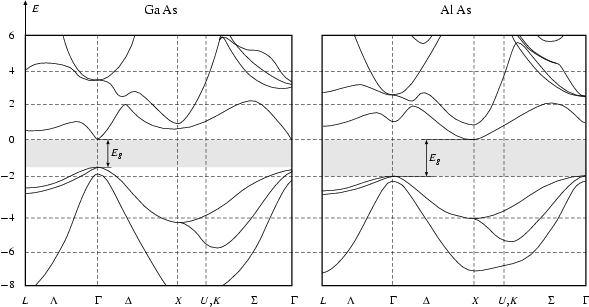
Die Tieftemperatur-Bandstrukturen von GaAs und
AlAs im rez...

Abbildung 1.5: Die Tieftemperatur-Bandstrukturen von

und

im reziproken Raum, aus Ibach und Lüth (1999) und Pavesi und Guzzi (1994). Die Null-Energie habe ich auf die untere Kante des Leitungsbandes gelegt.

Der linke Teil von Abbildung 1.5 zeigt die Bandstruktur von . In einem solchen Bänderschema sind die möglichen Energien von Elektronen (im Leitungsband, ) und Löchern (im Valenzband, ) dargestellt in Abhängigkeit vom Quasi-Impuls des Teilchens (≙ seinem Ort im reziproken Raum).

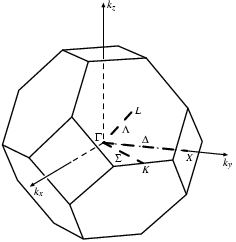
Die erste Brillouin-Zone eines fcc-Gitters, also des
GaAs-...

Abbildung 1.6: Die erste Brillouin-Zone eines fcc-Gitters, also des

-Gittertyps.

Um sich die Bedeutung der -Achse eines Bänderschemas besser vorstellen zu können, habe ich in Abbildung 1.6 die erste Brillouin-Zone des -Gitters aufgezeichnet, die die Form eines sogenannten Kub-Oktaeders hat. Der Γ-Punkt ist das Zentrum des reziproken Raumes, hier ist der Quasi-Impuls gleich Null. K, X und L sind weitere hochsymmetrische Punkte, wohingegen Δ, Σ und Λ verschiedene Strecken im reziproken Gitter kennzeichnen. Nach dieser Erläuterung komme ich jetzt wieder zurück zum Bänderschema.

Grau unterlegt ist die Bandlücke von . ist an derjenigen Stelle abgegriffen, wo Valenz- und Leitungsband an diese Lücke stoßen, dem Γ-Punkt. Es ist unschwer zu erkennen, daß diese Stellen genau übereinander liegen. heißt daher ein direkter Halbleiter. In Kapitel 4, wo ich die optischen Eigenschaften klären werde, werde ich darauf näher eingehen.

Aus einem solchen Bänderschema läßt sich jedoch noch mehr herauslesen. Nicht nur Maxima und Minima, besonders der Bänder direkt über bzw. unter der Bandlücke sind interessant. Auch die Krümmung der Bänder hat eine unmittelbare physikalische Bedeutung, sie ist nämlich umgekehrt proportional zur effektiven Masse des Lochs bzw. des Elektrons:

$m_{\text{eff}} = \frac{ℏ^2}{ⅆ^2E/ⅆk^2}.$

Wie ich später berichten werde, sammeln sich die Ladungsträger am Γ-Punkt. Dort sind die Kurvenkrümmungen offensichtlich besonders groß, also die effektiven Massen besonders klein (ungefähr

mal kleiner als natürlich). Das führt dann in der Schrödinger-Gleichung zu einem großen Laplace-Term und damit zu einer großen Energie, z. B. der Quantendraht-Zustände. (Groß im Vergleich zu einem freien Elektron in demselben Potential.)

Die effektiven Massen der Löcher sind etwas größer, außerdem gibt es am Γ-Punkt sogenannte leichte und schwere Löcher. Die schweren Löcher haben die kleinere Bandkrümmung und liegen energetisch höher. Der Lumineszenz-Übergang findet in erster Näherung zu den schweren Löchern statt, siehe aber Schwarz (2001, Kap. 13).

hat eine prinzipiell andere Bandstruktur als

, da es sich um einen indirekten Halbleiter handelt. Der tiefste Punkt des Leitungsbandes liegt jetzt nicht mehr am Γ-, sondern am X-Punkt. Im Materialsystem $Al_xGa_{1-x}As$ findet man aber erst für

einen indirekten Übergang, d. h. ich benutze in dieser Arbeit ausschließlich direkte Halbleiter. Die Bandlücke liegt bei

$E_g = (1,5194+1,36x+0,22x^2) \text{eV}, x<0,4 ,$

(Pavesi und Guzzi 1994). Für

bedeutet das

1.3 Eindimensionaler Transport

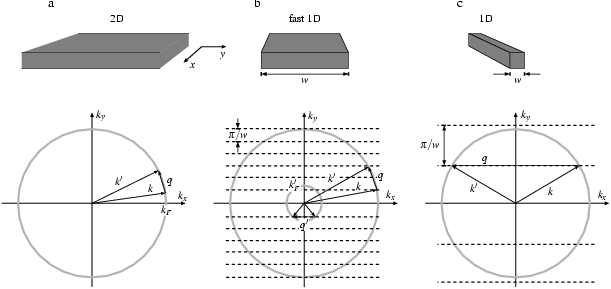
Illustration zu den möglichen
Streu-EreignissenStreuung in...

Abbildung 1.7: Illustration zu den möglichen Streu-Ereignissen in Einschluß-Potentialen verschiedener Dimensionalität. Aus Hartmann (1997)

Quantendrähte sind in das Blickfeld des Interesses gerückt, als man theoretisch in diesen Systemen eine hohe Beweglichkeit vorhergesagt hatte. Abbildung 1.7 zeigt grob, welche Überlegung dahinter steckt:

Links (Fall a) ist die Situation in einem zweidimensionalen Elektronengas (2DEG) aufgezeichnet. Im reziproken Raum besetzten die Elektronen, die den elektrischen Strom tragen können, die Zustände auf einem Kreis mit dem Radius (Fermikreis). Bei einem Streuprozeß (z. B. an einer ionisierten Störstelle) von nach wird meist nur ein geringer Impuls übertragen. Das ist in diesem Fall auch kein Problem, denn die Zustände liegen auf dem Fermikreis fast beliebig dicht.

Ich gehe nun zu Fall b über, indem ich das 2DEG in einer weiteren Raumdimension (in der Abbildung die -Richtung) auf die Breite einschränke. Die Wirkung davon zeigt das untere Teilbild: Die Zustände in -Richtung sind nun merklich quantisiert, es gibt auf dem Fermikreis nur noch mögliche Zustände, wo die gestrichelten Linien den Kreis schneiden.

Es sind aber immer noch genügend kleine möglich. Selbst wenn ich den Fermikreis durch Herabsetzen der Konzentration der Ladungsträger auf reduziere, bleiben die typischen Beträge für klein.

Anders sieht es aus, wenn ich so weit verkleinere, daß fast alle möglichen Werte für aus dem Fermikreis heraus gewandert sind (Fall c). Eine große Menge an Ladungsträgern vorausgesetzt, stehen nur noch recht große Werte für zur Verfügung, was die sogenannte Kleinwinkelstreuung an den Störstellen unterdrückt. Das wiederum soll zu der erhöhten Beweglichkeit führen.⁵⁾

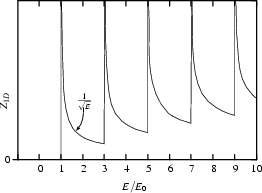
Abbildung 1.8: Eindimensionale Zustandsdichte

Die Abbildung 1.8 illustriert die Zustandsdichte für den eindimensionalen Fall. Im Gegensatz zum dreidimensionalen (Wurzelfunktion) und zweidimensionalen Fall (Stufenfunktion) findet man hier nahezu diskrete Energien, die besetzt werden können, sogenannte Subbänder. Das Ziel bei der Herstellung von Quantendrähten ist zum einen, das Fermilevel hoch genug zu bringen, so daß viele Subbänder mit Elektronen besetzt sind. Andererseits möchte man, daß die Subbänder einen großen Abstand voneinander haben, um eine Streuung zwischen ihnen so unwahrscheinlich wie möglich zu machen. In gewisser Weise ist das lediglich eine andere Sichtweise für das oben bereits gesagte. Für eine wesentlich tiefere Erklärung verweise ich auf Beenakker und van Houten (1991).

Neuere Arbeiten (Moško und Vagner 1999) bezweifeln allerdings diese erhöhten Beweglichkeiten und kommen im Gegenteil zu einer sehr niedrigen Beweglichkeit. Experimentell konnte man bislang noch keine der beiden Voraussagen bestätigen, weil noch keine Quantendrähte vorliegen, deren Qualität das zulassen würde.

Teil I:
Herstellung der Proben

Kapitel 2: Vorstrukturierung der V-Gräben

[…]

2.1 Ätzen der V-Gräben

[…]

2.1.1 Experimentelle Durchführung

Tabelle 2.1: Die einzelnen Schritte zum Ätzens der V-Gräben
Prozeßschritt	Chemikalien	Parameter


Vorreinigung
Spülen		ca.
Spülen		ca.
Ätzen
Spülen		ca.
Spülen		ca.
-Entfernung	$HF_{\text{(aq)}}$
Spülen		ca.

Die Probe T1139 nach dem Ätzen von ca. ... (Für Original-Bitmap anklicken)

Abbildung 2.1: Die Probe T1139 nach dem Ätzen von ca.

, bevor das

entfernt wurde

Zunächst wird ein Wafer in die vier Viertel aus Abbildung ?? gespalten. Alles folgende bezieht sich nun auf eines dieser Viertel.

Die Tabelle 2.1 gibt einen Überblick über die experimentellen Details des Ätzvorgangs. Das verwendete Brom hat die Reinheitsstufe „pro analysis“. Ich habe Brom in Methanol gelöst, man nennt es daher (etwas lax) -prozentiges (Brom-Methanol).

Die Ätzzeit von ist lediglich eine Richtzeit. Anhand der TEM-Strukturen auf dem Wafer kann man recht leicht die Tiefe der Ätzung abschätzen. Ich habe versucht, bei allen Wafern eine Ätzstufe (AS) von – zu erreichen, d. h. die breiten Gräben der TEM-Struktur sind zum Teil bereits V-förmig, zum Teil noch U-förmig. Eventuell wird dafür ein Nachätzen nötig.

Die Flußsäure dient nicht nur dazu, das zu lösen, sie besorgt auch die Endreinigung des Wafers vor der Bewachsung in der MOVPE. Insbesondere werden einige anorganische Rückstände (z. B. Oxide) gelöst, damit sie nicht das Wachstum auf den Seitenflächen stören können Kaluza (2000, Kap. 7.1).

Die Abbildung 2.1 zeigt ein positives Beispiel für ein geätztes Viertel. Die -Kanten sind einigermaßen glatt, entsprechendes gilt für die Seitenflächen der Gräben. (Man beachte, daß die Seitenflächen vor dem Bewachsen grundsätzlich wesentlich rauher erscheinen.) Man sieht keine Löcher, die durch Reste der Ätze verursacht werden können, und auch die Verschmutzungen halten sich sehr in Grenzen.

[…]

2.1.2 Versuch mit einer -Maske

[…]

Kapitel 3: Wachstum der Quantendrähte

[…]

3.1 Heterostrukturen

Es ist heute ein Standardverfahren, Schichten aus verschiedenen Halbleitern epitaktisch aufeinander abzuscheiden. Dabei sind nicht nur Reinkristalle möglich, sondern auch Strukturen mit einer statistischen Besetzung, z. B. $Al_xGa_{1-x}As$ , das für meine Arbeit eine ganz besondere Bedeutung hatte. Den Wert für kann man dabei beliebig zwischen und einstellen, also von reinem zu reinem übergehen.

Darüber hinaus ist es auch möglich, eine in gewissen Grenzen beliebige Dotierung in die Schicht einzubringen. In meiner Arbeit wird $Al_xGa_{1-x}As$ mit Silizium n-dotiert, d. h. das Silizium besetzt As-Gitterplätze, und zwar in Konzentrationen zwischen undotiert und $16·10^{17} cm^{-3}$ .

Verspannungen oder gar massive Kristalldefekte, die bei nicht aufeinander passenden Gittern entstehen können, sind in diesem Materialsystem kein Problem. Die Kristallklasse ist dieselbe und die Gitterkonstanten nahezu identisch.

3.1.1 Der Heteroübergang

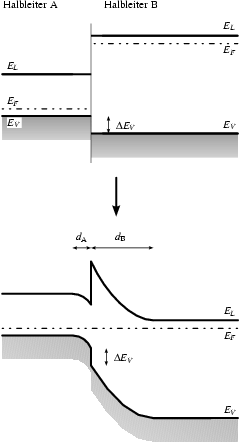
Abbildung 3.1: Räumlicher Bänderverlauf am Heteroübergang. Die Grenzschicht liegt an der Banddiskontinuität. Aus Ibach und Lüth (1999)

Unterschiedliche Halbleiter haben unterschiedliche Bandstrukturen, insbesondere andere Bandlücken, und das kann man z. B. zum Aufbau von Barrieren am Heteroübergang nutzen. Die Abbildung 3.1 zeigt stark vereinfacht, was an einem solchen Übergang passiert und welches Gleichgewicht sich einstellt:

Das obere Teilbild zeigt eine Situation, die, wenn überhaupt, nur ein infitesimal kurzes Zeitintervall lang besteht. Die beiden Halbleiter A und B sind gerade mit ihren perfekten Oberflächen aneinander gefügt worden (mit welchem Verfahren auch immer). Bei diesem Erstkontakt suchen die Bänder die richtige relative Lage zueinander. Die Bedingungen, die dabei erfüllt werden, sind recht kompliziert. Es stellt sich ein Valenzbandsprung

ein, der nur von den Materialien abhängt (nicht von der Dotierung) und experimentell bestimmt werden kann. Im Falle von A ≙

und B ≙

ist dieser Sprung beispielsweise (Ibach und Lüth 1999)

$Δ E_V\text{(GaAs—AlAs)}=0,34 \text{eV}.$

(Man beachte, daß

die größere Bandlücke hat.)

Das Fermi-Niveau ist jetzt aber in beiden Halbleitern unterschiedlich, was bedeutet, daß sich der Übergang nicht im Gleichgewicht befindet. Die Elektronen aus dem Halbleiter B, dessen größer ist, spüren eine Kraft in Richtung Halbleiter A, in dessen Grenzregion sich daher eine negative Raumladungszone der Tiefe $d_{\text A}$ ausbildet; umgekehrt lassen die Elektronen im Halbleiter B eine positive Raumladungszone der Tiefe $d_{\text B}$ zurück.

Das dadurch entstehende elektrische Feld, beziehungsweise dessen Potential, verbiegt die energetischen Bänder wie das untere Teilbild von Abbildung 3.1 zeigt. Die Bedingung, daß das Fermi-Niveau konstant ist, ist nun erfüllt. Man beachte, daß erhalten bleibt.

3.1.2 Modulationsdotierung

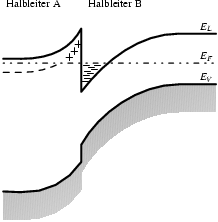
Abbildung 3.2: Räumlicher Bänderverlauf am modulationsdotierten Heteroübergang. Der Halbleiter A ist stark n-dotiert, Halbleiter B ist nur sehr schwach n-dotiert. Die Grenzschicht liegt an der Banddiskontinuität. Aus Ibach und Lüth (1999)

Die Abbildung 3.2 illustriert einen anderen wichtigen Fall: Der linke Halbleiter A ist nun stark n-dotiert. Die Donatoren liegen knapp unterhalb des Leitungsbandes (gestrichelte Linie). Die Bandverbiegung hat hier dazu geführt, daß das Fermi-Niveau teilweise über dem Leitungsband liegt. Diejenigen Donatoren, die über das Fermi-Niveau gezogen wurden, konnten ihr Elektron abgeben und sind positiv zurückgelassen worden (in der Zeichnung mit „“ markiert). Diese Elektronen sind in einem schmalen Bereich im Halbleiter B, der unter dem Fermi-Niveau liegt, eingesperrt („“ in der Zeichnung).

Durch diesen Trick ist es möglich, die Quellen der freien Ladungsträger, die Donatoren, von dem Gebiet, in dem sich die freien Ladungsträger aufhalten und eventuell bewegen, räumlich zu trennen. Die Donatoren sind Störstellen, und als solche verringern sie die Beweglichkeit der Elektronen. Das gilt besonders für tiefe Temperaturen, weil dann andere Streumechanismen (vor allem Phononen) kaum noch beitragen.

Für das zweidimensionale Elektronengas (2DEG), das sich im Halbleiter B direkt an der Grenzfläche ausbildet, gilt das nicht. Dessen Zustände ragen immer auch etwas in den Halbleiter A hinein, daher wird der Effekt durch eine sogenannte Spacer-Schicht zwischen der Donator-Schicht und dem 2DEG noch verstärkt. Mit derselben Methode werden auch in die V-Graben Quantendrähte die Ladungsträger gebracht.

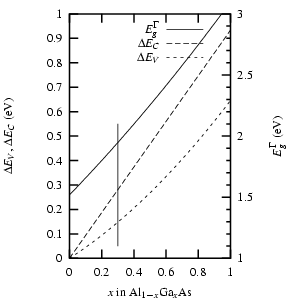
$Materialparameter im System Al_{1-x}Ga_xAs bei 0 K. Δ ...$

Abbildung 3.3: Materialparameter im System $Al_{1-x}Ga_xAs$ bei

und

beziehen sich auf einen Heteroübergang zu

ist die Bandlücke am Γ-Punkt, die für

nicht mehr die kleinste Lücke ist. Aus Hartmann (1997)

Die Abbildung 3.3 gibt abschließend noch einmal einen Überblick über die Parameter, die die Heteroübergänge von $Al_xGa_{1-x}As$ -Varianten beschreiben. Die senkrechte Linie steht für , der für meine Quantendraht-Schichten typische Wert.

3.2 Grundlagen der MOVPE

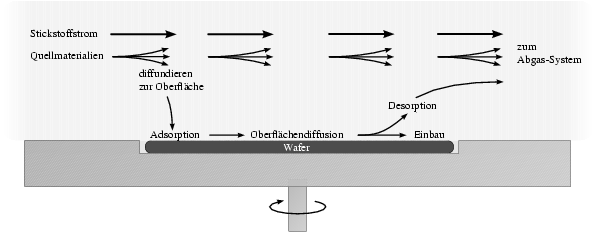
Abbildung 3.4: Schematischer Überblick über die physikalischen und chemischen Reaktionen, die in der MOVPE an der Substrat-Oberfläche stattfinden

Die metall-organische Gasphasen-Epitaxie MOVPE ist eine bewährte Methode, hochqualitative Halbleiterschichten auf entsprechende Substrate aufzubringen, und das in einer gut kontrollierbaren Art und Weise.

Als Quelle für die abzuscheidenden Materialien⁶⁾ dienen bestimmte Stoffe (im folgenden Quellverbindungen genannt), in denen das jeweilige Element-Atom in ein Molekül eingebettet ist. Meist sind das metall-organische Verbindungen wie z. B. Trimethyl-Gallium, auf jeden Fall jedoch Gase, die zusammen mit einem Trägergas wirbelfrei über die Substrat-Oberfläche strömen. Das Trägergas, in meinem Fall Stickstoff, nimmt an den chemischen Reaktionen nur als Katalysator teil (Schmidt 1998, Kap. 2.3). Schon im Trägergas-Strom, vor allem aber auf der Substrat-Oberfläche, spielen sich derweil sehr komplexe Prozesse ab, siehe Abbildung 3.4:

Damit überhaupt irgend etwas passiert, muß die Quellverbindung mit der Substrat-Oberfläche (≙ einem Wafer, bei mir meist einem -Viertelstückchen) erst einmal in Kontakt kommen. Es gibt dafür keinen gerichteten Mechanismus wie in der MBE. Allein die Diffusion der Quellengase innerhalb des Trägergases garantiert, daß an der Oberfläche stets Quellmaterial vorhanden ist.

Der zweite Schritt ist das Herauslösen des abzuscheidenden Elements aus dem Molekülverband. Das geschieht zum Teil schon innerhalb des Trägergases, vor allem aber auf der Substrat-Oberfläche. Die so befreiten Atome werden dann in die Kristallstruktur der Oberfläche eingebaut. Die Restmoleküle formen u. U. ebenfalls neue Verbindungen und entweichen wieder in das Trägergas, das sie dem Abgas-System der MOVPE-Anlage zuführt. In meinem Fall, also mit

für das Gallium,

für das Aluminium und

(Arsin) für das Arsen, ergibt sich insgesamt folgende Reaktion:

$x{\{(CH_3)_3Al\}}+(1-x){\{(CH...$

Soweit der grobe Überblick.

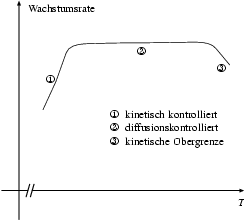
3.2.1 Diffusionskontrolliertes Wachstum

Abbildung 3.5: Die drei verschiedenen Temperaturbereiche des MOVPE-Wachstums.

Der ganze Abscheide-Prozeß in der MOVPE ist selbstverständlich ein statistischer Vorgang. Die intensiven thermodynamischen Größen, die eine Rolle spielen, sind die Partialdrücke der Materialien und deren Temperatur⁷⁾. Der gesamte Ablauf ist ja unterteilt in Zwischenschritte (Diffusion, Zerlegung, Einbau, …); die Temperatur bestimmt nun, welcher dieser Zwischenschritte limitierend wird.

Für meine Proben wurde die Anlage im diffusionskontrollierten Bereich betrieben (siehe Abbildung 3.5). In diesem Modus ist die Temperatur hoch genug, daß der Einbau auf der Substrat-Oberfläche sehr rasch abläuft. Die Diffusion hin zur Oberfläche zeigt sich jedoch von einer Erhöhung der Temperatur ziemlich unbeeindruckt und bremst die Gesamtreaktion aus. Andersherum ausgedrückt kontrolliert die Diffusion das Wachstum.

Die weitgehende Unabhängigkeit der Diffusion von der Temperatur ist gerade der Vorteil: Die Wachstumsrate reagiert recht unempfindlich auf zeitliche und räumliche Schwankungen der Temperatur des Substrates, die Schichtdicke ist folglich gut kontrollierbar und homogen.

In erster Näherung ist die Wachstumsrate in diesem Modus proportional zum Partialdruck des Gruppe-III-Materials. Das Gruppe-V-Material ist nämlich im hundertfachen Überschuß vorhanden und ist daher nicht limitierend.

Bei niedrigeren Temperaturen wechselt man in den kinetisch kontrollierten Bereich, bei dem die Zerlegung und der Einbau in die Kristallstruktur bremsen. Diese sind, typisch für chemische Reaktionen, stark abhängig von der Temperatur, was zu Unregelmäßigkeiten des Wachstums führt, die nicht mehr hinnehmbar sind.

Bei höheren Temperaturen (d. h. höher als beim diffusionskontrollierten Wachstum) wird die komplette Reaktion (Zerlegen, Einbau, …) thermodynamisch immer ungünstiger: Die Wachstumsrate nimmt mit der Temperatur wieder ab. Daher ist auch dieser Temperaturbereich nicht sinnvoll.

3.2.2 Diffusionsprozesse

Die Quellmaterialien seien zerlegt und auf dem Weg zurück in den Trägergas-Strom. Sie hinterließen auf der Waferoberfläche die Gallium- oder Arsenatome, die nun eingebaut werden sollen. Ihre Bindung mit dem Kristallverbund ist jedoch zunächst nur sehr schwach (verglichen mit einer Kristallbindung), sie sind lediglich adsorbiert. Der Grund dafür ist, daß sie nur sehr wenige nächste Nachbarn haben und das energetisch ausgesprochen ungünstig ist (große Oberflächen-Energie).

Sie können sich auf der Waferoberfläche ähnlich einer Diffusion bewegen, man nennt das daher Oberflächendiffusion. Es ist eine Suche nach dem Energie-Minimum, was zunächst einmal bedeutet, eine Stelle zu finden, wo die Zahl der nächsten Nachbarn groß ist. Das kann eine Stufe zwischen zwei Monolagen sein, oder auch eine Insel, die sich auf einer Monolage gebildet hat.

Große Diffusionslängen sind dabei ausgesprochen günstig. Die Atome sollten also stets eine Stufe erreichen können, ohne irgendwo auf einer Monolage zusammen mit einem anderen diffundierenden Atom der Kristallisationskeim für eine neue Insel zu werden. Inselwachstum führt nämlich zu einem Aufrauhen der Oberfläche, im Gegensatz zum Stufenfluß-Wachstum, das sich bei großen Diffusionslängen einstellt. Um Stufenfluß-Wachstum zu erreichen, darf eine bestimmte Temperatur nicht unterschritten werden.

3.3 Wachsen von Quantendrähten in der MOVPE

TEM-Bild der Probe 3083. Diese Probe ge... (Für Original-Bitmap anklicken)

Abbildung 3.6: TEM-Bild der Probe 3083. Diese Probe gehört nicht zu denen, die ich im Rahmen dieser Arbeit hergestellt habe, aber sie illustriert wegen ihres dickeren

-Kanals und des guten Kontrastes sehr gut die typischen Strukturen.

Die Herstellung von Quantendrähten in der MOVPE ist ein sehr aufwendiges Unterfangen. Das betrifft nicht den einzelnen Epitaxielauf, sondern die Bestimmung der optimalen Wachstumsparameter. Diese notwendige intensive Vorarbeit, die es mir ermöglichte, beinahe im Fließband-Verfahren Proben zu epitaxieren, verdanke ich Kaluza (2000) und Schwarz (2001).

Vergrößerung des TEM-Bildes der Probe 3... (Für Original-Bitmap anklicken)

Abbildung 3.7: Vergrößerung des TEM-Bildes der Probe 3083. Facettengrenzen habe ich durch weiße Punkte hervorgehoben.

Die Abbildung 3.6 zeigt eine TEM-Aufnahme, die einen sehr schönen Überblick über die einzelnen Strukturen gibt, die der

-Kanal ausbildet:

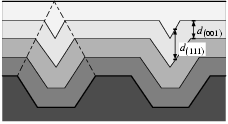
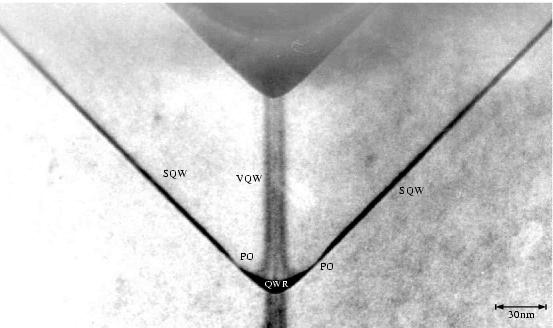
QWR:: Der Quantendraht (Quantum Wire, QWR) ist nach oben meist durch drei Facetten begrenzt, die in der Vergrößerung in Abbildung 3.7 schön zu sehen sind. Dies sind 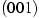(Mitte), 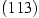, 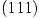und 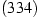(von innen nach außen). Nach unten gibt es auch mehrere Facetten (Schwarz 2001, Kap. 5.3.2), sie sind jedoch kaum zu erkennen.
SQW:: Die beiden Seiten-Quantentöpfe (Side Quantum Wells, SQWs) sind 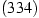-Facetten des 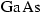-Gitters, was einen Winkel zur Waagrechten von ca. 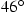bedeutet.
PO:: Die Abschnürung (Pinch-Off, PO) trennt den QWR vom SQW. Rechner-Simulationen in Kaluza (2000); Schwarz (2001) zeigen, daß der Einfluß der Abschnürung auf die elektronischen Zustände gering ist. Lediglich bei sehr hohen Zuständen, die im SQW liegen, ergeben sich kleine Unterschiede.
VQW:: Der vertikale Quantentopf (Vertical Quantum Well, VQW) ist eine Entmischung des 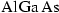, die auf den drei oberen Facetten des QWR anwächst (siehe Abbildung 3.7); daher bilden sich auch drei VQW-Stränge aus. In jedem Strang ist die Aluminium-Konzentration um ungefähr ein Drittel erniedrigt. In Schwarz (2001, Kap. 5.3.3) wird das Phänomen genauer beschrieben.
TQW:: Der obere Quantentopf (Top Quantum Well, TQW) ist in der Abbildung nicht zu sehen, er würde sich planar (in der Abbildung horizontal) links und rechts an die SQWs anschließen.

3.3.1 Wachsen auf V-Gräben

Wenn man auf einem nicht-planaren Wafer eine Epitaxie durchführt, wird die Beschreibung des Wachstums komplizierter, da man es nun mit verschiedenen Facetten zu tun hat. Zu jeder Facette gehört eine bestimmte Netzebene des Waferkristalls, und die Netzebenen wiederum verhalten sich verschieden, was den Einbau von Atomen aus der Gasphase angeht.

Sind die Diffusionslängen auf der Oberfläche sehr groß (viel größer als die Facettenbreiten), können sich die adsorbierten Atome den Platz, an dem sie eingebaut werden, aussuchen. In diesem Fall kann ich alle Facetten unabhängig betrachten und berücksichtige nur, wie leicht sich Atome jeweils einbauen lassen. Daraus erhalte ich eine feste Wachstumsrate für jede Facette.

Abbildung 3.8: Zum Wachstum auf V-Gräben

Abbildung 3.8 zeigt, was das für die V-Gräben bedeutet: Die Wachstumsrate (in senkrechter Richtung!) ist auf den -Facetten größer als auf den waagerechten -Facetten. Die Folge davon ist ein Zuwachsen der Gräben, wenn gewünscht bis hin zur Planarisierung.

Die unebene (≙ vorstrukturierte) Oberfläche ist natürlich größer als die planare und verbraucht daher auch mehr Material für das Wachstum. Wie oben bereits erklärt, ist die Wachstums-Geschwindigkeit im diffusionskontrollierten Regime dadurch bestimmt, wie schnell aus dem Gasstrom frisches Quellmaterial per Diffusion nachgeliefert werden kann. Im Falle einer unebenen Oberfläche wird dieser Flaschenhals relativ noch enger: Die Wachstumsrate ist für alle Facetten geringer, als es rein rechnerisch für die jeweiligen Wachstums-Parameter wäre. Dieser Effekt nimmt selbstverständlich ab, wenn die V-Gräben immer weiter zuwachsen.

3.3.2 Ausbilden des Quantendrahtes

[…]

3.4 Konkrete Epitaxien

Für die Epitaxie stand eine Anlage der Firma Aixtron vom Typ AIX-200 zur Verfügung. Sie wird in Kaluza (2000) und in dort aufgeführten Literaturstellen eingehend beschrieben.

Wie schon in Abschnitt 2.1.1 erwähnt, habe ich nur mit Wafervierteln gearbeitet. Jeweils ein vorstrukturiertes Viertel kam zusammen mit einem mit Flußsäure vorgereinigten -off-Waferviertel⁸⁾ in den Anlagenreaktor. Der Sinn des -off-Viertels besteht darin, daß es exakt dieselbe Schichtstruktur aufgewachsen bekommt, allerdings – von der Reinigung abgesehen – keine Vorprozessierung mitgemacht hat. Dadurch habe ich hier eine wohldefinierte Probe, die ich bei den Photolumineszenz-Messungen als Vergleich benutzen kann. Außerdem sollte sein Spektrum dem planaren Quantentopf der strukturierten Proben entsprechen, so daß man hier eine weitere Hilfe bei der Entschlüsselung des Spektrums der V-Graben-Strukturen hat.

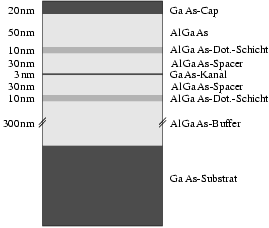
3.4.1 Schichtfolge

Abbildung 3.9: Eine für meine Proben typische Schichtfolge für eine MOVPE-Epitaxie

Die Abbildung 3.9 zeigt die Schichtfolge für meine Epitaxien. Exemplarisch habe ich eine dotierte Probe mit einem -Kanal von herausgegriffen. In der ganzen Arbeit bezeichnet die Kanaldicke die nominelle Kanaldicke des TQW, d. h. diejenige Schichtdicke des -Kanals, die sich ohne Vorstrukturierung ausbilden würde.

Von den -Buffer sind die unteren mit der alternativen Quelle Dimethyl-Ethyl-Amin-Alan (Alan, ) gewachsen. Das hat nur historische Gründe, da auf dieser Schicht leichter das polykristalline Wachstum auf den -Flächen beginnen kann (Schwarz 1997, Kap. 3.1.6). Da ich das grundsätzlich mit Flußsäure abgenommen habe, ist das für mich bedeutungslos.

Alle anderen Schichten wurden mit den Quellen /‚ und Arsin () bewachsen. Für eine eventuelle negative Dotierung des kam Silan () zum Einsatz.

3.4.2 Umfang der gewachsenen Proben

Tabelle 3.1: Ein Überblick über alle essentiellen Proben, die ich hergestellt habe.
Dotierung unten/oben	Kanaldicke


( $10^{17} cm^{-3}$ )

undotiert	T111	T112	T113	T114	T121
1/2	T141	T144	T141	T143	T163
2/4	T161	T162	T164	T151	T152
4/8	T153	T154	T171	T172
8/16	T192	T191	T193	T194	T214

Die Tabelle 3.1 enthält alle Proben, die Teil der Meßreihe sind, die den Kern dieser Arbeit ausmacht. Sie sind dort in Form einer Matrix aufgeführt, in Abhängigkeit von Dotierung und Kanaldicke (nominelle Schichtdicke des TQWs). Die Proben wurden chronologisch von geringer zu großer Dotierung hergestellt, innerhalb einer Dotierung meist binnen weniger Tage. Die Lücke rechts von T172 ist kein Versehen; eine Probe mit diesen Parametern wurde wegen eines betriebsbedingten Engpasses nie hergestellt.

3.5 TEM-Aufnahmen

TEM-Bild der Probe T1925 (Für Original-Bitmap anklicken)

Abbildung 3.10: TEM-Bild der Probe T1925

Abbildung 3.11: TEM-Bild der Probe T1925

Von einer meiner Proben, nämlich T192, wurden TEM-Aufnahmen gemacht, sowohl gewöhnliche Hellfeld-Abbildungen, als auch hochauf‌lösende Bilder. Leider läßt sich nicht rekonstruieren, auf welche Öffnungsweite der V-Gräben geschaut wurde, die Kanaldicke beträgt jedenfalls .

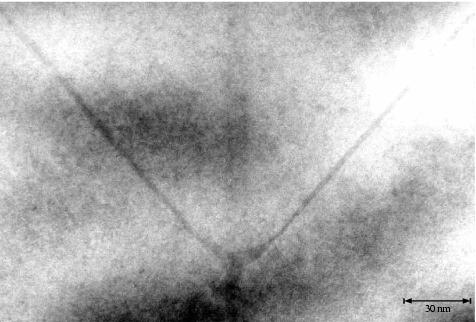
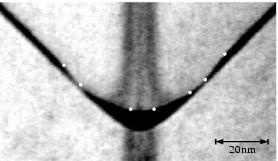
Die Abbildung 3.10 zeigt den Bereich einer V-Graben-Spitze. Man erkennt trotz des schwachen Kontrastes die Verdickung des QWRs, die Abschnürungen und selbstverständlich die SQWs zu beiden Seiten. Der VQW läßt sich höchstens erahnen.

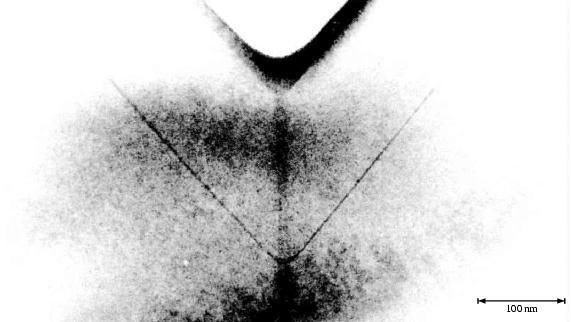
Dafür ist dieser auf der Abbildung 3.11 etwas besser zu sehen. Hier ist der gewählte Ausschnitt etwas größer, man kann bis zur Probenoberfläche schauen.

[…]

Die TEM-Aufnahmen dienen zwei Zwecken: Zum einen zeigen nur sie die gewachsenen Drahtstrukturen direkt und erlauben mir so, weitere Aussagen über die Qualität der gewachsenen Proben zu machen. Die Aufnahmen an sich sind zwar überwiegend von schwachem Kontrast oder grober Körnung, da die Untersuchung so kleiner Strukturen mit solch eng verwandten Materialien eine heikle Sache ist; sie zeigen jedoch, daß die Proben zumindest von der Qualität sind, die auch bisher in der benutzten MOVPE üblich gewesen ist. Zu sehen ist lediglich eine leichte Asymmetrie des QWRs, die rechte -Facette scheint ein wenig länger zu sein als ihr linkes Pendant.

[…]

Teil II:
Optische Untersuchungen

Kapitel 4: Vorbemerkungen

Halt er den rechten Pfropf bereit, wenn er das große Loch nicht scheut.

– Die Alte, Faust I

4.1 Photolumineszenz in Halbleitern

Materie kann auf elektromagnetische Strahlung auf verschiedene Arten reagieren. Die einfachste Möglichkeit ist sicherlich die Absorption und Umwandlung in Gitterschwingungen, was einfach zur thermischen Aufheizung führt. Sofortige Emission nach der Absorption⁹⁾ bedeutet Streuung (Brechung, Reflexion, …). Abhängig von Material und Wellenlänge gibt es aber auch noch andere Möglichkeiten.

Lumineszenz bedeutet, daß ein Photon dazu genutzt wird, ein Valenzelektron in einen wesentlich höheren energetischen Zustand zu bringen, welches dann, um wieder in eine stabile Lage zu kommen, einen Teil dieser absorbierten Energie in Form eines Photons größerer Wellenlänge wieder abgibt.

Typischerweise läuft das folgendermaßen ab: Das Elektron absorbiert das Photon und schießt in die höheren Regionen des Leitungsbandes. Der Aufenthalt dort ist höchst instabil. Es thermalisiert sich rasend schnell am Kristallgitter, d. h. es gibt seine Energie erst an optische Phononen ab, dann an akustische. Innerhalb von Pikosekunden läuft es so ein Leitungsband im -Raum herunter (Pavesi und Guzzi 1994). Bereits in dieser Phase kann es vorkommen, daß das Elektron mit einem Loch rekombiniert. Das ist dann „heiße Lumineszenz“. Außerdem können tiefe Störstellen in der Bandlücke dem Elektron eine Möglichkeit eröffnen, nicht-strahlend zu rekombinieren.

4.2 Band-Band-Übergang

Meistens jedoch schafft es das Elektron bis zu dem Minimum des Leitungsbandes. Von dort aus geht es erst einmal nicht weiter. Es befindet sich in einem meta-stabilen Zustand. Es dauert jetzt einige hundert Pikosekunden, bis es mit einem Loch, das zwischenzeitlich die Oberkante des Valenzbandes erreicht hat, rekombiniert. Von diesem Übergang spürt das Kristallgitter nichts, statt dessen wird die ganze Energie in ein Photon umgewandelt. Dessen Impuls, also die Richtung, in die es abgestrahlt wird, ist praktisch isotrop.¹⁰⁾ Allerdings muß es ja noch den Kristall irgendwie verlassen, und das geht nicht in jede Richtung gleich gut (das Bulk- wird das Photon beispielweise sofort wieder absorbieren). Dabei spielt auch die Oberflächen-Strukturierung der Probe eine wichtige Rolle.

Bei einem direkten Halbleiter wie ist diese strahlende Rekombination sehr leicht zu realisieren, weil das Elektron mit dem Loch bereits dieselbe Position im -Raum teilt. Bei indirekten Halbleitern (z. B. Silizium) benötigt das Elektron ein Phonon, das mit dem richtigen Impuls im richtigen Moment zur Stelle ist, um den -Sprung zum Loch zu realisieren. Dort ist die strahlende Rekombination ein eher unbedeutender Prozeß.

Für schwache Anregung ist die Form des Lumineszenz-Signals des Band-Band-Übergangs temperaturabhängig (entnommen aus Schmidt (1998)):

$I ∼ \sqrt{ℏω-E_g} exp{(-\frac{ℏω-E_g}{k_BT})}$

Dabei ist

die Energie des Lumineszenz-Lichts. $\sqrt{ℏω-E_g}$ repräsentiert die Zustandsdichte, der Exponential-Faktor die Verteilungsfunktion¹¹⁾. Der Peak verbreitert sich mit zunehmender Temperatur.

4.3 Leistungsabhängigkeit

In nullter Näherung gilt: Mehr eingestrahlte Lichtleistung führt zu mehr emittierter Lichtleistung. Das ist aber eine sehr vereinfachte Sicht der Dinge.

Sofern es die Intensität des Lumineszenz-Lichts betrifft, ist der beste Ansatz eine Potenzfunktion (Guimaraes 1992):

$I∼ P^t\text{.}$

Dabei ist

die anregende Lichtleistung. Für intrinsische Exzitonen-Übergänge erwartet man

(mit Oberflächen-Rekombination

), intrinsische Elektron-Loch-Übergänge sollten

ergeben. Da häufig mehrere Kanäle für die Rekombination offen sind, sind auch alle Zwischenwerte möglich. Guimaraes (1992) berichtet sogar von einem

bei einer

-Heterostruktur. Dennoch: Überwiegen exzitonische Rekombinationen, sollte

zu beobachten sein.

Exzitonen sind spezielle Anregungen der Elektronen im Festkörper. Dabei kommt es zu einem gebundenen Zustand eines Elektrons und eines Loches. Bei der Rekombination muß man die Bindungs-Energie von der reinen Rekombinations-Energie abziehen. (Guimaraes 1992)

[…]

4.4 Der eindimensionale Zustand

Grundsätzlich gilt für alle Überlegungen und Versuche dieser Arbeit, daß sie im thermodynamischen Gleichgewicht stattfinden. Ich muß daher nirgends eine Zeitabhängigkeit berücksichtigen.

Die stationäre Schrödinger-Gleichung des Elektrons in einem Potential

ist

$-\frac{ℏ^2}{2m_e}Δψ(→r) + V(→r)ψ(→r) = Eψ(→r)\text{.}$

Ist das Potential unabhängig von

(wie in einem idealisierten Quantendraht, der in

-Richtung verläuft), so kann man die

-Abhängigkeit in

abseparieren. Zunächst schreibt man

$ψ(x,y,z) ≕ φ(x,y)χ(z)\text{,}$

dann folgt aus Gleichung (4.1) nach Einsetzen von diesem

$-\frac{ℏ^2}{2m_e}\frac1φ{(\frac{∂^2φ}{∂ x^2} +\frac{∂^2φ}{∂ y^2})}+V=...$

(Beide Seiten habe ich durch

dividiert.) Die linke Seite ist jetzt nur noch von

und

abhängig, die rechte nur noch von

. Damit die Formel erfüllt sein kann, müssen also beide Seiten konstant und gleich sein; ich nenne diese Konstante $E_{xy}$ . Daraus ergeben sich die beiden Gleichungen

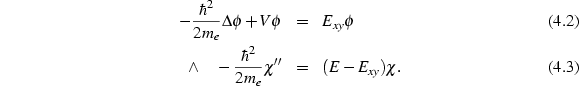
$-\frac{ℏ^2}{2m_e}Δφ+Vφ #=# E_{xy}φ ...$

Gleichung (4.3) ist die Schrödinger-Gleichung des freien Teilchens. Also gilt $E-E_{xy}=\frac{ℏ^2k_z^2}{2m_e}$ und schließlich

$E=E_{xy}+\frac{ℏ^2k_z^2}{2m_e}.$

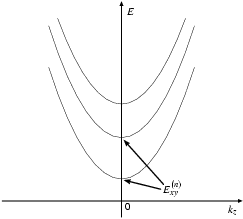
Illustration der Subbänder mit n=1,2,3 in einem
Quantendraht

Abbildung 4.1: Illustration der Subbänder mit

in einem Quantendraht

Gleichung (4.2) macht klar, wie man $E_{xy}$ interpretieren muß: Es ist die Energie, die sich bei einer rein zweidimensionalen Betrachtung des Quantendraht-Profils ergibt. Da die Form eines Potentialtopfes hat, liegen u. U. gebundene Zustände vor (auf jeden Fall nur eine endliche Zahl von ihnen), die jeweils eine diskrete Energie $E_{xy}^{(n)}$ haben. Insgesamt können Elektronen im Quantendraht die in Abbildung 4.1 eingezeichneten Energien haben. Die einzelnen Parabeln heißen Subbänder.

Im Halbleiterkristall muß man für die korrekte effektive Masse einsetzen.

Anhang A: Danksagungen

Ich danke

Herrn Prof. Dr. H. Lüth, der mir die Bearbeitung dieses sehr interessanten Themas im Rahmen dieser Arbeit an seinem Institut ermöglichte,
Herrn Prof. Dr. B. Lengeler für die Übernahme des Koreferats,
Priv.-Doz. Dr. Thomas Schäpers und Dr. Axel Schwarz für meine hervorragende Betreuung in Jülich und für die breite Hilfestellung auf dem Gebiet der V-Gräben,
Herrn Dr. R. Carius für die ausgezeichnete Betreuung aller optischen Messungen, sowohl was das experimentelle, als auch das theoretische betrifft,
Markus Hülsbeck, Herrn Dipl.-Ing. J. Klomfaß und Dipl.-Phys. Bernd Schuller für die kompetente Unterstützung im PL-Labor, ohne die die Messungen nicht möglich gewesen wären,
Dr. Andreas Kaluza für Antworten auf viele Fragen im Bereich V-Gräben und MOVPE,
Herrn K. Wirtz und Dr. Dorothea Gauer für die Durchführung der zahlreichen Epitaxien,
Frau D. Meertens und Frau Dr. M. Luysberg für die TEM-Aufnahmen und wichtige Details rund um die Transmissions-Elektronen-Mikroskopie,
Rakesh Roshan M.Sc. für die interessanten und angenehmen Aufenthalte in Oxford,
dem Reinraumteam für die Hilfestellung und das Instandsetzen der Einrichtungen, an denen ich gewütet hatte,
Herrn Dr. Paul Müller für die Kristallstrukturen in Kapitel 1,
Dipl.-Phys. Vitaly Guzenko, Frank Macheray, Dr. Pavel Vagner, Oliver Zimmermann und Dipl.-Phys. Jens Knobbe für viele anregende Diskussionen,
und allen, die sich angesprochen fühlen, für den Spaß, den wir hatten.

Außerdem: Don Knuth and Friends für TeX, LaTeX mit all seinen Zusatzpaketen und cweb, der FSF für die vielen kleinen Helferlein, insbesondere für den C++-Compiler, HP für die vielen guten Drucker, Robert Slimbach, Luc de Groot und Herrmann Zapf für die Schriftarten, die hier Verwendung fanden, (de.)comp.text.tex für viele lehrreiche Threads. Frau Werwolf für den hervorragenden Catering-Service, Frau Latten für den leckeren Kakao und die lockeren Sprüche. Dem FZJ dafür, daß ich im ISI meine Arbeit begann und im ISG abschloß, obwohl ich die ganze Zeit im IPV war. Herrn Dr. Hoffmann vom Institut für Angewandte Sprachwissenschaft der RWTH für seine Terminplanung, die mich ständig in Atem hielt. Frau Anja Prick von der Commerzbank und Herrn Gregor Surawicz von Bruker für die Visitenkarten, mit denen ich monatelang den Laser fand. Ludwig van Beethoven für alles, was er in c-moll und H-dur zustande gebracht hat. Douglas Adams für h2g2. RTL für 17.30–18.00 Uhr und die tollen Einlagen für Sam, PRO7 für den Montag abend. Harry dafür, daß er immer so hell geleuchtet hat. Mutter Natur für den direkten Bandübergang und dafür, daß ℏ so klein ist, sonst hätte es wohl auch ein Quantenkabel getan.

Literatur

Beenakker, C. W. J. und H. van Houten, 1991: Quantum Transport in Semiconductor Nanostructures. Solid State Physics: Advances in Research and Applications, 44, S. 1–228.

Borchardt-Ott, Walter, 1997: Kristallographie. Fünfte Auflage Aufl. Springer-Verlag.

Guimaraes, Francisco Eduardo Gontijo, 1992: Untersuchungen zur Photolumineszenz von Al{}_xGa{}_{1-x}As-Heterogrenzflächen aus der metall-organischen Gasphasenepitaxie. Doktorarbeit, Universität-Gesamthochschule Duisburg.

Hartmann, Arno, Aug. 1997: Wachstum von Halbleiter-Nanostrukturen auf strukturierten Substraten. Doktorarbeit, Institut für Schicht- und Ionentechnik Jülich.

Ibach, Harald und Hans Lüth, 1999: Festkörperphysik – Einführung in die Grundlagen. Dritte Aufl. Springer-Verlag, Berlin.

Kaluza, Andreas, 2000: MOVPE-Wachstum und Charakterisierung von V-Graben Quantendrähten im Materialsystem AlGaAs/GaAs. Doktorarbeit, RWTH Aachen.

Moško, Martin und Pavel Vagner, 1999: Born approximation versus the exact approach to carrier-impurity collisions in a one-dimensional semiconductor: Impact on the mobility. Physical Review B, 59, S. 10 445.

Pavesi, Lorenzo und Maria Guzzi, 1994: Photoluminescence of {}Al_xGa_{1-x}As. J. Appl. Phys., 75, S. 4779.

Schmidt, Roland, Febr. 1998: Beurteilung der optischen Eigenschaften von AlGaInP hergestellt in der metall-organischen Gasphasenepitaxie unter Stickstoff- oder Wasserstoffatmosphäre. Diplomarbeit, RWTH Aachen.

Schwarz, Axel, Sept. 1997: Magnetotransportmessungen an modulationsdotierten GaAs/Al{}_{1-x}Ga{}_xAs Quantendrähten in V-Gräben. Diplomarbeit, RWTH Aachen.

Schwarz, Axel, 2001: Wachstum und Charakterisierung von Halbleiternanostrukturen auf vorstrukturiertem Substrat. Doktorarbeit, RWTH Aachen.

Stichwortverzeichnis

[A] [B] [D] [E] [F] [G] [H] [I] [K] [L] [M] [N] [O] [P] [Q] [R] [S] [T] [V] [W] [Z]

Abschnürung 3.3

Aixtron 3.4

Ätzen 1.1

Ätzstufe 2.1.1

Band-Band-Übergang 4.2

Banddiskontinuität 3.1.2

Bänderschema 1.2

Bandlücke 3.1.2, 1.2

Bandstruktur 1.2

Beweglichkeit 3.1.2, 1.3, [hier]

Brechung 4.1

Diffusion 3.2

diffusionskontrolliertes Wachstum 3.2.1

Diffusionslänge 3.2.2, 3.3.1

Diffusionsprozesse der MOVPE 3.2.2

direkter Halbleiter 1.2, 4.2

Dotierung 3.1.2, 3.4.1, 3.4.1, 3.2, [hier]

Entmischung 3.3

Exzitonen 4.3

Facetten 3.3.1, 3.3

Fermi-Energie 3.1.1, 1.3

Fermikreis 1.3

Gitterkonstante 1.1

Hereroübergang 3.1.1

indirekter Halbleiter 1.2, 4.2

Inselwachstum 3.2.2

Inversionssymmetrie 1.1

Kleinwinkelstreuung 1.3

Kristalldefekte 3.1

Ladungsträger

– Konzentration [hier]

Leitungsband 1.2

Löcher 1.2

Lumineszenz 4.1

Materialparameter 3.1.2

Matrix 3.4.2

Modulationsdotierung 3.1.2

MOVPE 3.3

– Diffusionsprozesse 3.2.2

Netzebenen 3.3.1, 1.1

Oxide 2.1.1

Partialdruck 3.2.1

Photolumineszenz 4.1

Planarisierung 3.3.1

polykristallines Wachstum 3.4.1

Potentialtopf [hier]

Quasi-Impuls 1.2

Quellverbindungen 3.2

Raumgruppe 1.1

Raumladungszone 3.1.1

Raumrichtungen 1.1

Reflexion 4.1

Rekombination 4.2

reziproker Raum 1.2

Schichtfolge 3.4.1

Schrödinger-Gleichung 1.2, 4.4

Stickstoff 3.2

Störstelle 3.1.2, 1.3, 4.1

Streuung 3.1.2, 1.3, 4.1

Stufenfluß-Wachstum 3.2.2, 3.4

Subbänder 1.3, 4.4

Substrat-Temperatur 3.2.1

Symmetrie-Elemente 1.1

Temperatur

– des Substrates 3.2.1

Thermalisieren 4.1

Trägergas 3.2

Valenzband 1.2

Valenzbandsprung 3.1.1

Wachstum 3.3

– diffusionskontrolliertes 3.2.1

– kinetisch kontrolliertes 3.2.1

– polykristallines 3.4.1

Wachstumsrate 3.2.1, 3.3.1, 3.3.1

Zustände

– im Quantendraht [hier]

Zustandsdichte 1.3

¹⁾ Man berechne das Skalarprodukt!

²⁾ Das sind Drehachsen, bei denen beide Richtungen unterschieden werden können.

³⁾ Dafür sind wohl auch die Bindungsverhältnisse verantwortlich.

⁴⁾ die Gitterkonstante wird über der Legierungs-Zusammensetzung linear interpoliert

⁵⁾ Einen eindimensionalen Zustand im engeren Sinne habe ich jedoch erst, wenn

so klein geworden ist, daß nur noch

möglich ist.

⁶⁾ Für meine Proben waren das Gallium, Aluminium, Arsen und eventuell Silizium für eine Dotierung.

⁷⁾ Die Temperaturen des Substrates sowie der Gase unmittelbar über dem Substrat werden als gleich angenommen und heißen im folgenden (Substrat-)Temperatur.

⁸⁾ Das sind Wafer, deren polierte Oberfläche um

gegen die

-Netzebene verkippt ist. Das begünstigt das Stufenfluß-Wachstum, da hier viele Stufen für einen Einbau vorhanden sind.

⁹⁾ mit derselben Photonenenergie!

¹⁰⁾ Photonen tragen ohnehin nur einen sehr kleinen Impuls.

¹¹⁾ angenähert durch eine Boltzmann-Verteilung