Kapitel 4: Vorbemerkungen

4.1 Photolumineszenz in Halbleitern

Materie kann auf elektromagnetische Strahlung auf verschiedene Arten reagieren. Die einfachste Möglichkeit ist sicherlich die Absorption und Umwandlung in Gitterschwingungen, was einfach zur thermischen Aufheizung führt. Sofortige Emission nach der Absorption⁹⁾ bedeutet Streuung (Brechung, Reflexion, …). Abhängig von Material und Wellenlänge gibt es aber auch noch andere Möglichkeiten.

Lumineszenz bedeutet, daß ein Photon dazu genutzt wird, ein Valenzelektron in einen wesentlich höheren energetischen Zustand zu bringen, welches dann, um wieder in eine stabile Lage zu kommen, einen Teil dieser absorbierten Energie in Form eines Photons größerer Wellenlänge wieder abgibt.

Typischerweise läuft das folgendermaßen ab: Das Elektron absorbiert das Photon und schießt in die höheren Regionen des Leitungsbandes. Der Aufenthalt dort ist höchst instabil. Es thermalisiert sich rasend schnell am Kristallgitter, d. h. es gibt seine Energie erst an optische Phononen ab, dann an akustische. Innerhalb von Pikosekunden läuft es so ein Leitungsband im -Raum herunter (Pavesi und Guzzi 1994). Bereits in dieser Phase kann es vorkommen, daß das Elektron mit einem Loch rekombiniert. Das ist dann „heiße Lumineszenz“. Außerdem können tiefe Störstellen in der Bandlücke dem Elektron eine Möglichkeit eröffnen, nicht-strahlend zu rekombinieren.

4.2 Band-Band-Übergang

Meistens jedoch schafft es das Elektron bis zu dem Minimum des Leitungsbandes. Von dort aus geht es erst einmal nicht weiter. Es befindet sich in einem meta-stabilen Zustand. Es dauert jetzt einige hundert Pikosekunden, bis es mit einem Loch, das zwischenzeitlich die Oberkante des Valenzbandes erreicht hat, rekombiniert. Von diesem Übergang spürt das Kristallgitter nichts, statt dessen wird die ganze Energie in ein Photon umgewandelt. Dessen Impuls, also die Richtung, in die es abgestrahlt wird, ist praktisch isotrop.¹⁰⁾ Allerdings muß es ja noch den Kristall irgendwie verlassen, und das geht nicht in jede Richtung gleich gut (das Bulk- wird das Photon beispielweise sofort wieder absorbieren). Dabei spielt auch die Oberflächen-Strukturierung der Probe eine wichtige Rolle.

Bei einem direkten Halbleiter wie ist diese strahlende Rekombination sehr leicht zu realisieren, weil das Elektron mit dem Loch bereits dieselbe Position im -Raum teilt. Bei indirekten Halbleitern (z. B. Silizium) benötigt das Elektron ein Phonon, das mit dem richtigen Impuls im richtigen Moment zur Stelle ist, um den -Sprung zum Loch zu realisieren. Dort ist die strahlende Rekombination ein eher unbedeutender Prozeß.

Für schwache Anregung ist die Form des Lumineszenz-Signals des Band-Band-Übergangs temperaturabhängig (entnommen aus Schmidt (1998)):

Dabei ist die Energie des Lumineszenz-Lichts. repräsentiert die Zustandsdichte, der Exponential-Faktor die Verteilungsfunktion¹¹⁾. Der Peak verbreitert sich mit zunehmender Temperatur.

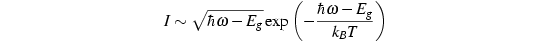
4.3 Leistungsabhängigkeit

In nullter Näherung gilt: Mehr eingestrahlte Lichtleistung führt zu mehr emittierter Lichtleistung. Das ist aber eine sehr vereinfachte Sicht der Dinge.

Sofern es die Intensität des Lumineszenz-Lichts betrifft, ist der beste Ansatz eine Potenzfunktion (Guimaraes 1992):

Dabei ist die anregende Lichtleistung. Für intrinsische Exzitonen-Übergänge erwartet man (mit Oberflächen-Rekombination ), intrinsische Elektron-Loch-Übergänge sollten ergeben. Da häufig mehrere Kanäle für die Rekombination offen sind, sind auch alle Zwischenwerte möglich. Guimaraes (1992) berichtet sogar von einem bei einer -/-Heterostruktur. Dennoch: Überwiegen exzitonische Rekombinationen, sollte zu beobachten sein.

Exzitonen sind spezielle Anregungen der Elektronen im Festkörper. Dabei kommt es zu einem gebundenen Zustand eines Elektrons und eines Loches. Bei der Rekombination muß man die Bindungs-Energie von der reinen Rekombinations-Energie abziehen. (Guimaraes 1992)

[…]

4.4 Der eindimensionale Zustand

Grundsätzlich gilt für alle Überlegungen und Versuche dieser Arbeit, daß sie im thermodynamischen Gleichgewicht stattfinden. Ich muß daher nirgends eine Zeitabhängigkeit berücksichtigen.

Die stationäre Schrödinger-Gleichung des Elektrons in einem Potential ist

Ist das Potential unabhängig von (wie in einem idealisierten Quantendraht, der in -Richtung verläuft), so kann man die -Abhängigkeit in abseparieren. Zunächst schreibt man

dann folgt aus Gleichung (4.1) nach Einsetzen von diesem

(Beide Seiten habe ich durch dividiert.) Die linke Seite ist jetzt nur noch von und abhängig, die rechte nur noch von . Damit die Formel erfüllt sein kann, müssen also beide Seiten konstant und gleich sein; ich nenne diese Konstante . Daraus ergeben sich die beiden Gleichungen

Gleichung (4.3) ist die Schrödinger-Gleichung des freien Teilchens. Also gilt und schließlich

Abbildung 4.1:Illustration der Subbänder mit in einem Quantendraht

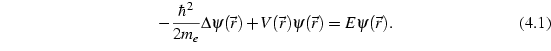
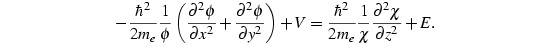
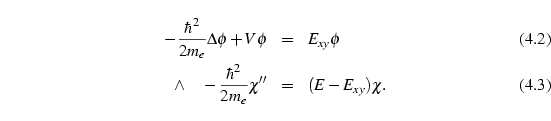
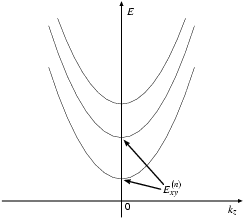
Gleichung (4.2) macht klar, wie man interpretieren muß: Es ist die Energie, die sich bei einer rein zweidimensionalen Betrachtung des Quantendraht-Profils ergibt. Da die Form eines Potentialtopfes hat, liegen u. U. gebundene Zustände vor (auf jeden Fall nur eine endliche Zahl von ihnen), die jeweils eine diskrete Energie haben. Insgesamt können Elektronen im Quantendraht die in Abbildung 4.1 eingezeichneten Energien haben. Die einzelnen Parabeln heißen Subbänder.

Im Halbleiterkristall muß man für die korrekte effektive Masse einsetzen.