Kapitel 3: Wachstum der Quantendrähte
[…]
3.1 Heterostrukturen
Es ist heute ein Standardverfahren, Schichten aus verschiedenen
Halbleitern epitaktisch aufeinander abzuscheiden. Dabei sind nicht nur
Reinkristalle möglich, sondern auch Strukturen mit einer statistischen
Besetzung, z. B. ![]() , das für meine Arbeit eine ganz
besondere Bedeutung hatte. Den Wert für
, das für meine Arbeit eine ganz
besondere Bedeutung hatte. Den Wert für ![]() kann man dabei beliebig
zwischen
kann man dabei beliebig
zwischen ![]() und
und ![]() einstellen, also von reinem
einstellen, also von reinem ![]() zu
reinem
zu
reinem ![]() übergehen.
übergehen.
Darüber hinaus ist es auch möglich, eine in gewissen Grenzen
beliebige Dotierung in die Schicht einzubringen. In meiner Arbeit wird
![]() mit Silizium n-dotiert, d. h. das Silizium besetzt
As-Gitterplätze, und zwar in Konzentrationen zwischen undotiert und
mit Silizium n-dotiert, d. h. das Silizium besetzt
As-Gitterplätze, und zwar in Konzentrationen zwischen undotiert und
![]() .
.
Verspannungen oder gar massive Kristalldefekte, die bei nicht aufeinander passenden Gittern entstehen können, sind in diesem Materialsystem kein Problem. Die Kristallklasse ist dieselbe und die Gitterkonstanten nahezu identisch.
3.1.1 Der Heterouebergang
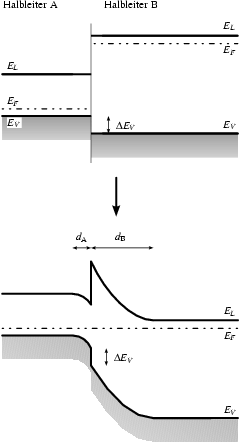
Unterschiedliche Halbleiter haben unterschiedliche Bandstrukturen, insbesondere andere Bandlücken, und das kann man z. B. zum Aufbau von Barrieren am Heterouebergang nutzen. Die Abbildung 3.1 zeigt stark vereinfacht, was an einem solchen Übergang passiert und welches Gleichgewicht sich einstellt:
Das Fermi-Niveau ![]() ist jetzt aber
in beiden Halbleitern unterschiedlich, was bedeutet, daß sich der Übergang
nicht im Gleichgewicht befindet. Die Elektronen aus dem Halbleiter B,
dessen
ist jetzt aber
in beiden Halbleitern unterschiedlich, was bedeutet, daß sich der Übergang
nicht im Gleichgewicht befindet. Die Elektronen aus dem Halbleiter B,
dessen ![]() größer ist, spüren eine Kraft in Richtung Halbleiter A,
in dessen Grenzregion sich daher eine negative Raumladungszone der
Tiefe
größer ist, spüren eine Kraft in Richtung Halbleiter A,
in dessen Grenzregion sich daher eine negative Raumladungszone der
Tiefe ![]() ausbildet; umgekehrt lassen die Elektronen im
Halbleiter B eine positive Raumladungszone der Tiefe
ausbildet; umgekehrt lassen die Elektronen im
Halbleiter B eine positive Raumladungszone der Tiefe ![]() zurück.
zurück.
Das dadurch entstehende elektrische Feld, beziehungsweise dessen
Potential, verbiegt die energetischen Bänder wie das untere Teilbild von Abbildung 3.1 zeigt. Die Bedingung, daß das
Fermi-Niveau ![]() konstant ist, ist nun erfüllt. Man beachte, daß
konstant ist, ist nun erfüllt. Man beachte, daß
![]() erhalten bleibt.
erhalten bleibt.
3.1.2 Modulationsdotierung
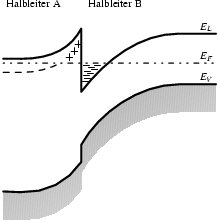
Die Abbildung 3.2 illustriert einen anderen
wichtigen Fall: Der linke Halbleiter A ist nun stark n-dotiert. Die
Donatoren liegen knapp unterhalb des Leitungsbandes ![]() (gestrichelte Linie). Die Bandverbiegung hat hier dazu geführt, daß das
Fermi-Niveau teilweise über dem Leitungsband liegt. Diejenigen Donatoren, die
über das Fermi-Niveau gezogen wurden, konnten ihr Elektron abgeben und sind
positiv zurückgelassen worden (in der Zeichnung mit „
(gestrichelte Linie). Die Bandverbiegung hat hier dazu geführt, daß das
Fermi-Niveau teilweise über dem Leitungsband liegt. Diejenigen Donatoren, die
über das Fermi-Niveau gezogen wurden, konnten ihr Elektron abgeben und sind
positiv zurückgelassen worden (in der Zeichnung mit „![]() “
markiert). Diese Elektronen sind in einem schmalen Bereich im
Halbleiter B, der unter dem Fermi-Niveau liegt, eingesperrt
(„
“
markiert). Diese Elektronen sind in einem schmalen Bereich im
Halbleiter B, der unter dem Fermi-Niveau liegt, eingesperrt
(„![]() “ in der Zeichnung).
“ in der Zeichnung).
Durch diesen Trick ist es möglich, die Quellen der freien Ladungsträger, die Donatoren, von dem Gebiet, in dem sich die freien Ladungsträger aufhalten und eventuell bewegen, räumlich zu trennen. Die Donatoren sind Störstellen, und als solche verringern sie die Beweglichkeit der Elektronen. Das gilt besonders für tiefe Temperaturen, weil dann andere Streumechanismen (vor allem Phononen) kaum noch beitragen.
Für das zweidimensionale Elektronengas (2DEG), das sich im Halbleiter B direkt an der Grenzfläche ausbildet, gilt das nicht. Dessen Zustände ragen immer auch etwas in den Halbleiter A hinein, daher wird der Effekt durch eine sogenannte Spacer-Schicht zwischen der Donator-Schicht und dem 2DEG noch verstärkt. Mit derselben Methode werden auch in die V-Graben Quantendrähte die Ladungsträger gebracht.
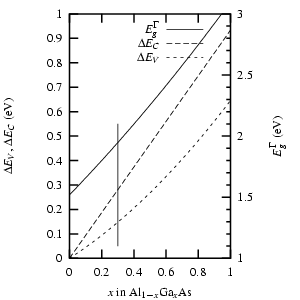
Die Abbildung 3.3 gibt
abschließend noch einmal einen Überblick über die Parameter, die die
Heteroübergänge von ![]() -Varianten beschreiben. Die
senkrechte Linie steht für
-Varianten beschreiben. Die
senkrechte Linie steht für ![]() , der für meine
Quantendraht-Schichten typische Wert.
, der für meine
Quantendraht-Schichten typische Wert.
3.2 Grundlagen der MOVPE
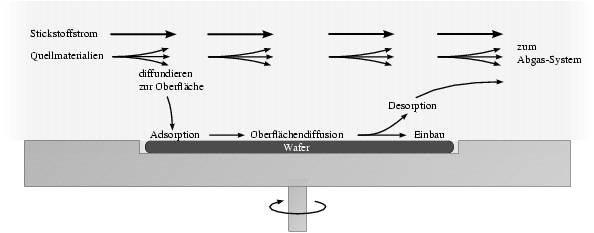
Die metall-organische Gasphasen-Epitaxie MOVPE ist eine bewährte Methode, hochqualitative Halbleiterschichten auf entsprechende Substrate aufzubringen, und das in einer gut kontrollierbaren Art und Weise.
Als Quelle für die abzuscheidenden Materialien6) dienen bestimmte Stoffe (im folgenden Quellverbindungen genannt), in denen das jeweilige Element-Atom in ein Molekül eingebettet ist. Meist sind das metall-organische Verbindungen wie z. B. Trimethyl-Gallium, auf jeden Fall jedoch Gase, die zusammen mit einem Trägergas wirbelfrei über die Substrat-Oberfläche strömen. Das Trägergas, in meinem Fall Stickstoff, nimmt an den chemischen Reaktionen nur als Katalysator teil (Schmidt 1998, Kap. 2.3). Schon im Trägergas-Strom, vor allem aber auf der Substrat-Oberfläche, spielen sich derweil sehr komplexe Prozesse ab, siehe Abbildung 3.4:
Damit überhaupt irgend etwas passiert, muß die Quellverbindung mit
der Substrat-Oberfläche (≙ einem Wafer, bei mir meist einem
![]() -Viertelstückchen) erst einmal in Kontakt kommen. Es gibt dafür
keinen gerichteten Mechanismus wie in der MBE. Allein
die Diffusion der Quellengase innerhalb des Trägergases garantiert,
daß an der Oberfläche stets Quellmaterial vorhanden ist.
-Viertelstückchen) erst einmal in Kontakt kommen. Es gibt dafür
keinen gerichteten Mechanismus wie in der MBE. Allein
die Diffusion der Quellengase innerhalb des Trägergases garantiert,
daß an der Oberfläche stets Quellmaterial vorhanden ist.
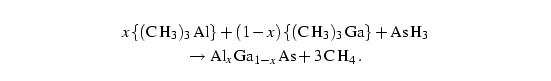
Soweit der grobe Überblick.
3.2.1 Diffusionskontrolliertes Wachstum
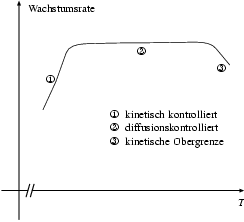
Der ganze Abscheide-Prozeß in der MOVPE ist selbstverständlich ein statistischer Vorgang. Die intensiven thermodynamischen Größen, die eine Rolle spielen, sind die Partialdrücke der Materialien und deren Temperatur7). Der gesamte Ablauf ist ja unterteilt in Zwischenschritte (Diffusion, Zerlegung, Einbau, …); die Temperatur bestimmt nun, welcher dieser Zwischenschritte limitierend wird.
Für meine Proben wurde die Anlage im diffusionskontrollierten Bereich betrieben (siehe Abbildung 3.5). In diesem Modus ist die Temperatur hoch genug, daß der Einbau auf der Substrat-Oberfläche sehr rasch abläuft. Die Diffusion hin zur Oberfläche zeigt sich jedoch von einer Erhöhung der Temperatur ziemlich unbeeindruckt und bremst die Gesamtreaktion aus. Andersherum ausgedrückt kontrolliert die Diffusion das Wachstum.
Die weitgehende Unabhängigkeit der Diffusion von der Temperatur ist gerade der Vorteil: Die Wachstumsrate reagiert recht unempfindlich auf zeitliche und räumliche Schwankungen der Temperatur des Substrates, die Schichtdicke ist folglich gut kontrollierbar und homogen.
In erster Näherung ist die Wachstumsrate in diesem Modus proportional zum Partialdruck des Gruppe-III-Materials. Das Gruppe-V-Material ist nämlich im hundertfachen Überschuß vorhanden und ist daher nicht limitierend.
Bei niedrigeren Temperaturen wechselt man in den kinetisch kontrollierten Bereich, bei dem die Zerlegung und der Einbau in die Kristallstruktur bremsen. Diese sind, typisch für chemische Reaktionen, stark abhängig von der Temperatur, was zu Unregelmäßigkeiten des Wachstums führt, die nicht mehr hinnehmbar sind.
Bei höheren Temperaturen (d. h. höher als beim diffusionskontrollierten Wachstum) wird die komplette Reaktion (Zerlegen, Einbau, …) thermodynamisch immer ungünstiger: Die Wachstumsrate nimmt mit der Temperatur wieder ab. Daher ist auch dieser Temperaturbereich nicht sinnvoll.
3.2.2 Diffusionsprozesse
Die Quellmaterialien seien zerlegt und auf dem Weg zurück in den Trägergas-Strom. Sie hinterließen auf der Waferoberfläche die Gallium- oder Arsenatome, die nun eingebaut werden sollen. Ihre Bindung mit dem Kristallverbund ist jedoch zunächst nur sehr schwach (verglichen mit einer Kristallbindung), sie sind lediglich adsorbiert. Der Grund dafür ist, daß sie nur sehr wenige nächste Nachbarn haben und das energetisch ausgesprochen ungünstig ist (große Oberflächen-Energie).
Sie können sich auf der Waferoberfläche ähnlich einer Diffusion bewegen, man nennt das daher Oberflächendiffusion. Es ist eine Suche nach dem Energie-Minimum, was zunächst einmal bedeutet, eine Stelle zu finden, wo die Zahl der nächsten Nachbarn groß ist. Das kann eine Stufe zwischen zwei Monolagen sein, oder auch eine Insel, die sich auf einer Monolage gebildet hat.
Große Diffusionslängen sind dabei ausgesprochen günstig. Die Atome sollten also stets eine Stufe erreichen können, ohne irgendwo auf einer Monolage zusammen mit einem anderen diffundierenden Atom der Kristallisationskeim für eine neue Insel zu werden. Inselwachstum führt nämlich zu einem Aufrauhen der Oberfläche, im Gegensatz zum Stufenfluß-Wachstum, das sich bei großen Diffusionslängen einstellt. Um Stufenfluß-Wachstum zu erreichen, darf eine bestimmte Temperatur nicht unterschritten werden.
3.3 Wachsen von Quantendrähten in der MOVPE
Die Herstellung von Quantendrähten in der MOVPE ist ein sehr aufwendiges Unterfangen. Das betrifft nicht den einzelnen Epitaxielauf, sondern die Bestimmung der optimalen Wachstumsparameter. Diese notwendige intensive Vorarbeit, die es mir ermöglichte, beinahe im Fließband-Verfahren Proben zu epitaxieren, verdanke ich Kaluza (2000) und Schwarz (2001).
- QWR:
- Der Quantendraht (Quantum Wire, QWR) ist
nach oben meist durch drei Facetten begrenzt, die in der
Vergrößerung in Abbildung 3.7 schön zu sehen sind. Dies
sind
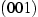 (Mitte),
(Mitte), 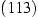 ,
, 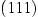 und
und 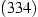 (von innen nach außen). Nach unten gibt es auch mehrere Facetten (Schwarz 2001, Kap. 5.3.2), sie sind jedoch kaum
zu erkennen.
(von innen nach außen). Nach unten gibt es auch mehrere Facetten (Schwarz 2001, Kap. 5.3.2), sie sind jedoch kaum
zu erkennen. - SQW:
- Die beiden Seiten-Quantentöpfe (Side
Quantum Wells, SQWs) sind
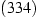 -Facetten des
-Facetten des  -Gitters, was
einen Winkel zur Waagrechten von ca.
-Gitters, was
einen Winkel zur Waagrechten von ca. 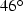 bedeutet.
bedeutet. - PO:
- Die Abschnürung (Pinch-Off, PO) trennt den QWR vom SQW. Rechner-Simulationen in Kaluza (2000); Schwarz (2001) zeigen, daß der Einfluß der Abschnürung auf die elektronischen Zustände gering ist. Lediglich bei sehr hohen Zuständen, die im SQW liegen, ergeben sich kleine Unterschiede.
- VQW:
- Der vertikale Quantentopf
(Vertical Quantum Well, VQW) ist eine Entmischung des
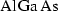 , die auf den drei oberen Facetten des QWR anwächst (siehe Abbildung 3.7); daher bilden sich auch drei VQW-Stränge aus. In
jedem Strang ist die Aluminium-Konzentration um ungefähr ein Drittel
erniedrigt. In Schwarz (2001, Kap. 5.3.3) wird das
Phänomen genauer beschrieben.
, die auf den drei oberen Facetten des QWR anwächst (siehe Abbildung 3.7); daher bilden sich auch drei VQW-Stränge aus. In
jedem Strang ist die Aluminium-Konzentration um ungefähr ein Drittel
erniedrigt. In Schwarz (2001, Kap. 5.3.3) wird das
Phänomen genauer beschrieben. - TQW:
- Der obere Quantentopf (Top Quantum Well, TQW) ist in der Abbildung nicht zu sehen, er würde sich planar (in der Abbildung horizontal) links und rechts an die SQWs anschließen.
3.3.1 Wachsen auf V-Gräben
Wenn man auf einem nicht-planaren Wafer eine Epitaxie durchführt, wird die Beschreibung des Wachstums komplizierter, da man es nun mit verschiedenen Facetten zu tun hat. Zu jeder Facette gehört eine bestimmte Netzebene des Waferkristalls, und die Netzebenen wiederum verhalten sich verschieden, was den Einbau von Atomen aus der Gasphase angeht.
Sind die Diffusionslängen auf der Oberfläche sehr groß (viel größer als die Facettenbreiten), können sich die adsorbierten Atome den Platz, an dem sie eingebaut werden, aussuchen. In diesem Fall kann ich alle Facetten unabhängig betrachten und berücksichtige nur, wie leicht sich Atome jeweils einbauen lassen. Daraus erhalte ich eine feste Wachstumsrate für jede Facette.

Abbildung 3.8 zeigt, was das für die
V-Gräben bedeutet: Die Wachstumsrate (in senkrechter Richtung!)
ist auf den ![]() -Facetten größer als auf den waagerechten
-Facetten größer als auf den waagerechten ![]() -Facetten. Die Folge davon ist ein Zuwachsen der Gräben, wenn gewünscht
bis hin zur Planarisierung.
-Facetten. Die Folge davon ist ein Zuwachsen der Gräben, wenn gewünscht
bis hin zur Planarisierung.
Die unebene (≙ vorstrukturierte) Oberfläche ist natürlich größer als die planare und verbraucht daher auch mehr Material für das Wachstum. Wie oben bereits erklärt, ist die Wachstums-Geschwindigkeit im diffusionskontrollierten Regime dadurch bestimmt, wie schnell aus dem Gasstrom frisches Quellmaterial per Diffusion nachgeliefert werden kann. Im Falle einer unebenen Oberfläche wird dieser Flaschenhals relativ noch enger: Die Wachstumsrate ist für alle Facetten geringer, als es rein rechnerisch für die jeweiligen Wachstums-Parameter wäre. Dieser Effekt nimmt selbstverständlich ab, wenn die V-Gräben immer weiter zuwachsen.
3.3.2 Ausbilden des Quantendrahtes
[…]
3.4 Konkrete Epitaxien
Für die Epitaxie stand eine Anlage der Firma Aixtron vom Typ AIX-200 zur Verfügung. Sie wird in Kaluza (2000) und in dort aufgeführten Literaturstellen eingehend beschrieben.
Wie schon in Abschnitt 2.1.1 erwähnt, habe ich nur mit
Wafervierteln gearbeitet. Jeweils ein
vorstrukturiertes Viertel kam zusammen mit einem mit Flußsäure vorgereinigten
![]() -off-Waferviertel8) in den Anlagenreaktor. Der Sinn des
-off-Waferviertel8) in den Anlagenreaktor. Der Sinn des
![]() -off-Viertels besteht darin, daß es exakt dieselbe Schichtstruktur
aufgewachsen bekommt, allerdings – von der Reinigung abgesehen –
keine Vorprozessierung mitgemacht hat. Dadurch habe ich hier eine
wohldefinierte Probe, die ich bei den Photolumineszenz-Messungen als Vergleich
benutzen kann. Außerdem sollte sein Spektrum dem planaren Quantentopf der
strukturierten Proben entsprechen, so daß man hier eine weitere Hilfe bei der
Entschlüsselung des Spektrums der V-Graben-Strukturen hat.
-off-Viertels besteht darin, daß es exakt dieselbe Schichtstruktur
aufgewachsen bekommt, allerdings – von der Reinigung abgesehen –
keine Vorprozessierung mitgemacht hat. Dadurch habe ich hier eine
wohldefinierte Probe, die ich bei den Photolumineszenz-Messungen als Vergleich
benutzen kann. Außerdem sollte sein Spektrum dem planaren Quantentopf der
strukturierten Proben entsprechen, so daß man hier eine weitere Hilfe bei der
Entschlüsselung des Spektrums der V-Graben-Strukturen hat.
3.4.1 Schichtfolge
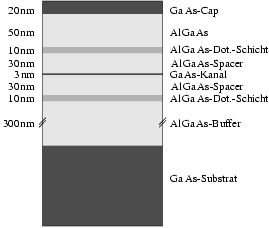
Die Abbildung 3.9 zeigt die Schichtfolge für meine
Epitaxien. Exemplarisch habe ich eine dotierte Probe mit einem
![]() -Kanal von
-Kanal von ![]() herausgegriffen. In der ganzen Arbeit
bezeichnet die Kanaldicke die nominelle Kanaldicke des TQW, d. h.
diejenige Schichtdicke des
herausgegriffen. In der ganzen Arbeit
bezeichnet die Kanaldicke die nominelle Kanaldicke des TQW, d. h.
diejenige Schichtdicke des ![]() -Kanals, die sich ohne
Vorstrukturierung ausbilden würde.
-Kanals, die sich ohne
Vorstrukturierung ausbilden würde.
Von den ![]()
![]() -Buffer sind die
unteren
-Buffer sind die
unteren ![]() mit der alternativen Quelle Dimethyl-Ethyl-Amin-Alan
(Alan,
mit der alternativen Quelle Dimethyl-Ethyl-Amin-Alan
(Alan, ![]() ) gewachsen. Das hat nur historische
Gründe, da auf dieser Schicht leichter das polykristalline Wachstum auf den
) gewachsen. Das hat nur historische
Gründe, da auf dieser Schicht leichter das polykristalline Wachstum auf den
![]() -Flächen beginnen kann (Schwarz 1997, Kap. 3.1.6). Da ich das
-Flächen beginnen kann (Schwarz 1997, Kap. 3.1.6). Da ich das ![]() grundsätzlich
mit Flußsäure abgenommen habe, ist das für mich bedeutungslos.
grundsätzlich
mit Flußsäure abgenommen habe, ist das für mich bedeutungslos.
Alle anderen Schichten wurden mit den Quellen
![]() /
/![]() und Arsin (
und Arsin (![]() ) bewachsen. Für eine
eventuelle negative Dotierung des
) bewachsen. Für eine
eventuelle negative Dotierung des ![]() kam Silan (
kam Silan (![]() )
zum Einsatz.
)
zum Einsatz.
3.4.2 Umfang der gewachsenen Proben
| Dotierung unten/oben | Kanaldicke | ||||
|---|---|---|---|---|---|
| ( |
|||||
| undotiert | T111 | T112 | T113 | T114 | T121 |
| 1/2 | T141 | T144 | T141 | T143 | T163 |
| 2/4 | T161 | T162 | T164 | T151 | T152 |
| 4/8 | T153 | T154 | T171 | T172 | |
| 8/16 | T192 | T191 | T193 | T194 | T214 |
Die Tabelle 3.1 enthält alle Proben, die Teil der Meßreihe sind, die den Kern dieser Arbeit ausmacht. Sie sind dort in Form einer Matrix aufgeführt, in Abhängigkeit von Dotierung und Kanaldicke (nominelle Schichtdicke des TQWs). Die Proben wurden chronologisch von geringer zu großer Dotierung hergestellt, innerhalb einer Dotierung meist binnen weniger Tage. Die Lücke rechts von T172 ist kein Versehen; eine Probe mit diesen Parametern wurde wegen eines betriebsbedingten Engpasses nie hergestellt.
3.5 TEM-Aufnahmen
Von einer meiner Proben, nämlich T192, wurden TEM-Aufnahmen
gemacht, sowohl gewöhnliche Hellfeld-Abbildungen, als auch hochauflösende
Bilder. Leider läßt sich nicht
rekonstruieren, auf welche Öffnungsweite der V-Gräben geschaut wurde, die
Kanaldicke beträgt jedenfalls ![]() .
.
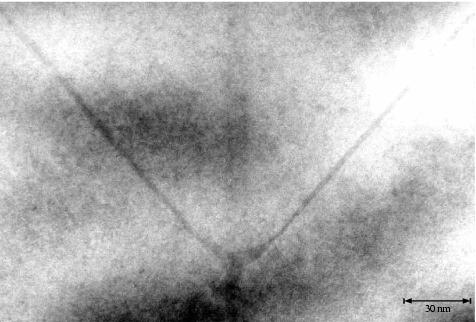
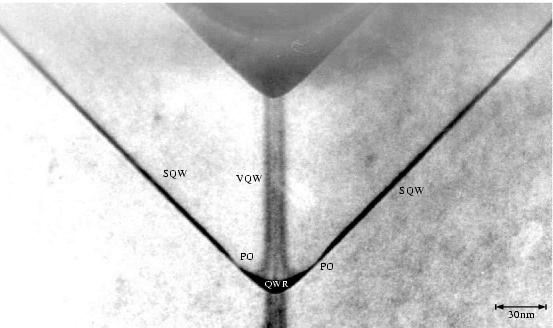
Die Abbildung 3.10 zeigt den Bereich einer V-Graben-Spitze. Man erkennt trotz des schwachen Kontrastes die Verdickung des QWRs, die Abschnürungen und selbstverständlich die SQWs zu beiden Seiten. Der VQW läßt sich höchstens erahnen.
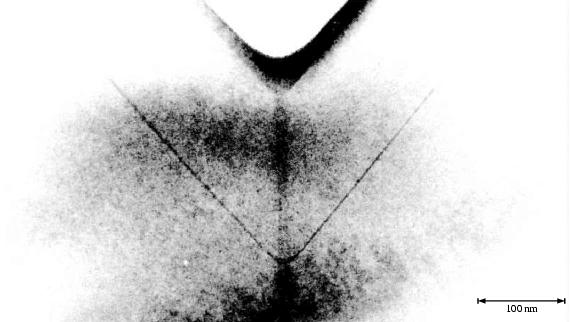
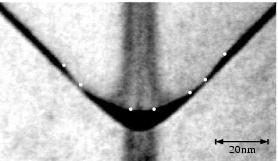
Dafür ist dieser auf der Abbildung 3.11 etwas besser zu sehen. Hier ist der gewählte Ausschnitt etwas größer, man kann bis zur Probenoberfläche schauen.
[…]
Die TEM-Aufnahmen dienen zwei Zwecken: Zum einen zeigen nur sie
die gewachsenen Drahtstrukturen direkt und erlauben mir so, weitere Aussagen
über die Qualität der gewachsenen Proben zu machen. Die Aufnahmen an sich sind
zwar überwiegend von schwachem Kontrast oder grober Körnung, da die
Untersuchung so kleiner Strukturen mit solch eng verwandten Materialien eine
heikle Sache ist; sie zeigen jedoch, daß die Proben zumindest von der Qualität
sind, die auch bisher in der benutzten MOVPE üblich gewesen ist. Zu sehen ist
lediglich eine leichte Asymmetrie des QWRs, die rechte ![]() -Facette
scheint ein wenig länger zu sein als ihr linkes Pendant.
-Facette
scheint ein wenig länger zu sein als ihr linkes Pendant.
[…]