Kapitel 1: Physikalische Grundlagen

1.1 Die Kristallstruktur von GaAs

Abbildung 1.1:Die Elementarzelle von . (Die Kugeln reräsentieren nicht die Atomradien; die geben lediglich die Lage der Schwerpunkte an.)

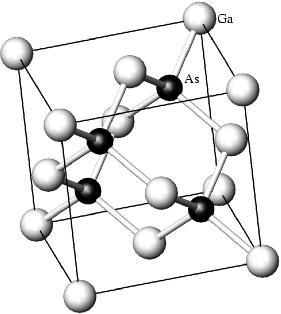
In Abbildung 1.1 sieht man die Elementarzelle von . Sie zeigt ein kubisch-flächenzentriertes (fcc‑)Gitter, Raumgruppe . Es gibt zwei Punktlagen: Das Gallium-Atom liegt auf , das Arsen-Atom auf . Sowohl das Gallium, als auch das Arsen bilden für sich ein kubisch flächenzentriertes Gitter, die beide gegeneinander um verschoben sind. (Siehe dazu auch Borchardt-Ott (1997).) Abbildung 1.1 zeigt die Elementarzelle, so wie sie in der Literatur meist dargestellt wird, aber man sollte beachten, daß man Ga und As gedanklich in der Struktur austauschen kann.

Bei allen Netzebenen und bei allen Raumrichtungen, die ich in dieser Arbeit angebe, verwende ich die Reihenfolge bzw. , wobei in allen Abbildungen senkrecht nach oben weist und auch senkrecht zum Wafer steht. Die Waferoberfläche ist also eine -Fläche. Alle Netzebenen der Form liegen parallel zur -Richtung,¹⁾ also derjenigen Richtung, in die die V-Gräben geätzt werden, und eine solche Netzebene schließt mit der Waferoberfläche einen Winkel ϑ ein mit

Abbildung 1.2:Symmetrie-Elemente der Punktgruppe . Die zwei verschiedenen Symbole für die dreizähligen Achsen deuten an, daß diese Achsen zwei verschiedene Enden besitzen, also polar sind; das gilt ebenso für die , obwohl nur ein Symbol. Aus Borchardt-Ott (1997, Kap. 7.1)

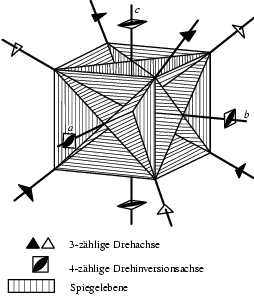
Die für Arbeiten mit Wafern wichtigsten Symmetrie-Elemente sind diejenigen, die senkrecht zur -Fläche liegen. Wie Abbildung 1.2 zeigt, gibt es drei dieser Art: Zwei Spiegelebenen, die auf dem Wafer in - und -Richtung verlaufen, sowie eine vierzählige Drehinversions-Achse  in -Richtung. Eine enthält keine vierzählige, nur eine zweizählige Drehachse. Das ist der Grund, warum V-Gräben nur in -Richtung, nicht aber senkrecht dazu, geätzt werden können. Es gibt ausschließlich polare Drehachsen²⁾ und damit keine Inversionssymmetrie.

Doch nach welchem Mechanismus werden überhaupt die V-Gräben ausgebildet? Ohne die Beschreibung des Ätzens in Abschnitt 2.1 vorwegzunehmen, möchte ich hier auf die kristallographischen Aspekte eingehen.

Abbildung 1.3:Blick in die Schichtstruktur von . Am Ga erkennt man die typische Schichtfolge A–B–C–A. Oben rechts ist eine Ga-Netzebene.

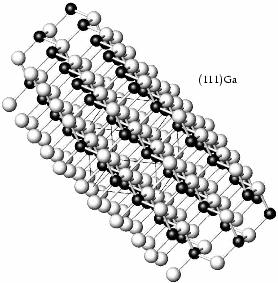
Abbildung 1.3 zeigt einen -Kristall fast senkrecht zur -Ebene. Damit ist diese Ansicht nicht ganz, aber fast in Richtung der V-Gräben. Man erkennt eine Schichtstruktur aus abwechselnd Gallium- und Arsen-Schichten. Oben rechts ist eine Ga-Netzebene, was bedeutet, daß es eine -Ebene ist, die mit Gallium-Atomen abschließt. Von dort wirkt auch die Ätze. Sie stoppt auf einer solchen Ga-Ebene, weil offensichtlich die Ga-Atome stärker als die As-Atome gebunden sind, was aus der Abbildung auch unmittelbar einsichtig wird: Jedes Ga-Atom wird von drei As-Atomen gehalten, wenn wir uns aber die oberste Ga-Schicht wegdenken, hätte jedes As-Atom nur ein Ga als nächsten Nachbarn. (Senkrecht zur -Ebene steht übrigens eine dreizählige Drehachse, die dadurch, daß sie polar ist, diese Asymmetrie überhaupt erst möglich macht.)

Es gibt allerdings auch rein chemische Gründe für dieses Verhalten, d. h. Gallium wird grundsätzlich wesentlich weniger stark von der Ätze gelöst als Arsen. Ätzt man V-Gräben in -Richtung, so stoppt der Vorgang nicht auf einer As-Ebene, obwohl dort die Bindungsverhältnisse äquivalent zu einer Ga-Ebene sind. Statt dessen wird extrem unterätzt bis zur nächsten Ga, die wegen der identisch zu einer Ga ist. (Kaluza 2000, Kap. 7.1)

Für das Ätzen von V-Gräben ist offensichtlich ebenfalls essentiell, daß eine -Ebene viel schneller als eine Ga-Ebene geätzt wird.³⁾ Anderenfalls müßte man extrem lange ätzen (und zahlreiche Defekte in Kauf nehmen), oder man würde sogar überhaupt keine V-Gräben erhalten.

Abbildung 1.4:Eine in eine -Struktur geätzte Kerbe, abgeschlossen von zwei -Netzebenen. Ich habe zur besseren Übersicht die vorderen Kanten hervorgehoben.

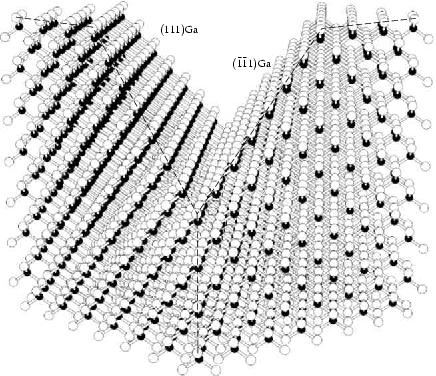
Die Abbildung 1.4 schließlich illustriert das Ergebnis eines typischen Ätzschrittes. Man sieht einen Würfel bestehend aus Elementarzellen, und wir schauen ungefähr in -Richtung, also über die Flächendiagonale des Würfels. Genau dort hat die Ätze gewirkt und einen V-Graben entstehen lassen, der von zwei äquivalenten Ga-Ebenen begrenzt ist (im Graben steht eine Spiegelebene!).

Im ist natürlich nur Gallium durch Aluminium zu ersetzen. Die Gitterkonstante von ist bei Zimmertemperatur um lediglich größer als die von . Ich benutze allerdings kein , sondern . Nimmt man das Vegardsche Gesetz an,⁴⁾ wird der Unterschied noch kleiner.

1.2 Die elektronische Struktur von GaAs

Abbildung 1.5:Die Tieftemperatur-Bandstrukturen von und im reziproken Raum, aus Ibach und Lüth (1999) und Pavesi und Guzzi (1994). Die Null-Energie habe ich auf die untere Kante des Leitungsbandes gelegt.

Der linke Teil von Abbildung 1.5 zeigt die Bandstruktur von . In einem solchen Bänderschema sind die möglichen Energien von Elektronen (im Leitungsband, ) und Löchern (im Valenzband, ) dargestellt in Abhängigkeit vom Quasi-Impuls des Teilchens (≙ seinem Ort im reziproken Raum).

Abbildung 1.6:Die erste Brillouin-Zone eines fcc-Gitters, also des -Gittertyps.

Um sich die Bedeutung der -Achse eines Bänderschemas besser vorstellen zu können, habe ich in Abbildung 1.6 die erste Brillouin-Zone des -Gitters aufgezeichnet, die die Form eines sogenannten Kub-Oktaeders hat. Der Γ-Punkt ist das Zentrum des reziproken Raumes, hier ist der Quasi-Impuls gleich Null. K, X und L sind weitere hochsymmetrische Punkte, wohingegen Δ, Σ und Λ verschiedene Strecken im reziproken Gitter kennzeichnen. Nach dieser Erläuterung komme ich jetzt wieder zurück zum Bänderschema.

Grau unterlegt ist die Bandlücke von . ist an derjenigen Stelle abgegriffen, wo Valenz- und Leitungsband an diese Lücke stoßen, dem Γ-Punkt. Es ist unschwer zu erkennen, daß diese Stellen genau übereinander liegen. heißt daher ein direkter Halbleiter. In Kapitel 4, wo ich die optischen Eigenschaften klären werde, werde ich darauf näher eingehen.

Aus einem solchen Bänderschema läßt sich jedoch noch mehr herauslesen. Nicht nur Maxima und Minima, besonders der Bänder direkt über bzw. unter der Bandlücke sind interessant. Auch die Krümmung der Bänder hat eine unmittelbare physikalische Bedeutung, sie ist nämlich umgekehrt proportional zur effektiven Masse des Lochs bzw. des Elektrons:

Wie ich später berichten werde, sammeln sich die Ladungsträger am Γ-Punkt. Dort sind die Kurvenkrümmungen offensichtlich besonders groß, also die effektiven Massen besonders klein (ungefähr mal kleiner als natürlich). Das führt dann in der Schrödinger-Gleichung zu einem großen Laplace-Term und damit zu einer großen Energie, z. B. der Quantendraht-Zustände. (Groß im Vergleich zu einem freien Elektron in demselben Potential.)

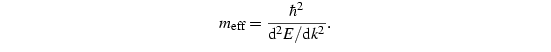
Die effektiven Massen der Löcher sind etwas größer, außerdem gibt es am Γ-Punkt sogenannte leichte und schwere Löcher. Die schweren Löcher haben die kleinere Bandkrümmung und liegen energetisch höher. Der Lumineszenz-Übergang findet in erster Näherung zu den schweren Löchern statt, siehe aber Schwarz (2001, Kap. 13).

hat eine prinzipiell andere Bandstruktur als , da es sich um einen indirekten Halbleiter handelt. Der tiefste Punkt des Leitungsbandes liegt jetzt nicht mehr am Γ-, sondern am X-Punkt. Im Materialsystem findet man aber erst für einen indirekten Übergang, d. h. ich benutze in dieser Arbeit ausschließlich direkte Halbleiter. Die Bandlücke liegt bei

(Pavesi und Guzzi 1994). Für bedeutet das . [An example of the <unit> element for physical quantities. It may also get more complicated, as in .]

1.3 Eindimensionaler Transport

Abbildung 1.7:Illustration zu den möglichen Streu-Ereignissen in Einschluß-Potentialen verschiedener Dimensionalität. Aus Hartmann (1997)

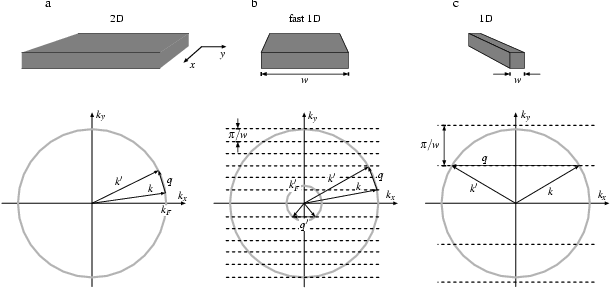
Quantendrähte sind in das Blickfeld des Interesses gerückt, als man theoretisch in diesen Systemen eine hohe Beweglichkeit vorhergesagt hatte. Abbildung 1.7 zeigt grob, welche Überlegung dahinter steckt:

Links (Fall a) ist die Situation in einem zweidimensionalen Elektronengas (2DEG) aufgezeichnet. Im reziproken Raum besetzten die Elektronen, die den elektrischen Strom tragen können, die Zustände auf einem Kreis mit dem Radius (Fermikreis). Bei einem Streuprozeß (z. B. an einer ionisierten Störstelle) von nach wird meist nur ein geringer Impuls übertragen. Das ist in diesem Fall auch kein Problem, denn die Zustände liegen auf dem Fermikreis fast beliebig dicht.

Ich gehe nun zu Fall b über, indem ich das 2DEG in einer weiteren Raumdimension (in der Abbildung die -Richtung) auf die Breite einschränke. Die Wirkung davon zeigt das untere Teilbild: Die Zustände in -Richtung sind nun merklich quantisiert, es gibt auf dem Fermikreis nur noch mögliche Zustände, wo die gestrichelten Linien den Kreis schneiden.

Es sind aber immer noch genügend kleine möglich. Selbst wenn ich den Fermikreis durch Herabsetzen der Konzentration der Ladungsträger auf reduziere, bleiben die typischen Beträge für klein.

Anders sieht es aus, wenn ich so weit verkleinere, daß fast alle möglichen Werte für aus dem Fermikreis heraus gewandert sind (Fall c). Eine große Menge an Ladungsträgern vorausgesetzt, stehen nur noch recht große Werte für zur Verfügung, was die sogenannte Kleinwinkelstreuung an den Störstellen unterdrückt. Das wiederum soll zu der erhöhten Beweglichkeit führen.⁵⁾

Abbildung 1.8:Eindimensionale Zustandsdichte

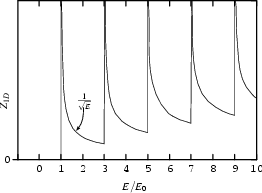
Die Abbildung 1.8 illustriert die Zustandsdichte für den eindimensionalen Fall. Im Gegensatz zum dreidimensionalen (Wurzelfunktion) und zweidimensionalen Fall (Stufenfunktion) findet man hier nahezu diskrete Energien, die besetzt werden können, sogenannte Subbänder. Das Ziel bei der Herstellung von Quantendrähten ist zum einen, das Fermilevel hoch genug zu bringen, so daß viele Subbänder mit Elektronen besetzt sind. Andererseits möchte man, daß die Subbänder einen großen Abstand voneinander haben, um eine Streuung zwischen ihnen so unwahrscheinlich wie möglich zu machen. In gewisser Weise ist das lediglich eine andere Sichtweise für das oben bereits gesagte. Für eine wesentlich tiefere Erklärung verweise ich auf Beenakker und van Houten (1991).

Neuere Arbeiten (Moško und Vagner 1999) bezweifeln allerdings diese erhöhten Beweglichkeiten und kommen im Gegenteil zu einer sehr niedrigen Beweglichkeit. Experimentell konnte man bislang noch keine der beiden Voraussagen bestätigen, weil noch keine Quantendrähte vorliegen, deren Qualität das zulassen würde.